Veidų išskyrimas

1. Veidų išskyrimo ir atpažinimo uždaviniai
2. Veidų skaitmeniniai signalai
3. Veidų išskyrimo metodikos
4. Violos ir Jones greitas veidų išskyrimo algoritmas
5. Hausdorfo metrikos panaudojimas išskirti veidams
6. Nuorodos
7. Praktinis darbas
8. Literatūra

Veidų išskyrimo ir atpažinimo uždaviniai

Kelių dešimčių metų kompiuterinio atpažinimo patirtis rodo, kad veidų ir kalbos uždaviniai yra vieni sunkesnių. Atpažinti kalbą kompiuteriu buvo pradėta kiek anksčiau, nes kalbos signalai reikalauja mažiau kompiuterio resursų, o kompiuterių eros pradžioje tai buvo aktualu. Pvz. vidutiniškai per 0.1 sekundę ištariamas vienas žodis. Kad išsaugoti šią informaciją telefono kokybės lygyje reikės 0.1x8000x1 = 800 baitų (0.1 sek., 8000 imčių per sek., 1 baitas imčiai). Palyginimui nedidelis nespalvotas paveikslėlis 200x200x1 = 40000 (200 taškelių plotis, 200 aukštis, 1 baitas pilkumo lygmeniui koduoti) pareikalaus 50 kartų daugiau kompiuterio resursų.

Šis faktas atsispindi ir mūsų smegenų žievės plotų funkciniame pasiskirstyme. Teigiama, kad apie 80 procentų smegenų žievės ploto skirta priimti ir apdoroti su vaizdais ir susijusią informaciją. Savo ruožtu smegenų dalis, kuri apdoroja vaizdus, yra specializuota veidų atpažinimui. Prisiminkite kiek iš veido pažįstate žmonių ir galėsite susidaryti įspūdį kokio atminties kiekio jums reikia šios unikalios informacijos įsiminimui.

Reikia skirti objekto išskyrimo ir atpažinimo uždavinius. Turint konkretų vaizdą pirma reikia išskirti lokalias sritis, kuriose yra veidai, o po to kiekvienoje srityje išskirtą veidą atpažinti priskiriant jį konkrečiam jums pažįstamam asmeniui arba nustatyti veido apibendrintus parametrus (rasę, lytį, amžių ir pan.). Kalbant programavimo kalbos Java terminais reikia skirti klases ir objektus. Klasės yra apibendrinti objektai, kuriuose apibrėžiami tos klasės objektus charakterizuojantys laukai. Veido išskyrimo uždavinys atitinka klasės tipo atpažinimą, o veido atpažinimas - objekto laukų reikšmių identifikavimą. Žinant objekto laukų reikšmes ir turint veidų "duomenų bazę" (mums pažįstamų veidų aibę) galima bandyti objektą sutapatinti su vienu iš bazėje esančių objektų arba priimti sprendimą, kad išskirto veido parametrai (požymiai) neatitinka nei vieną mums pažįstamą. Šiame kurse mes mėginsime spręsti tik pirmąjį uždavinį, t.y. veido(-ų) išskyrimo uždavinį.

Veidų skaitmeniniai signalai

Kaip ir kalbos atveju reikia skirti analoginius, diskrečiuosius ir skaitmeninius vaizdus.

Analoginis vaizdas matematine prasme yra dviejų kintamųjų funkcija

u   =   u(x,y).

(x,y) plokščio vaizdo taškelio (angl. pixel - "picture element" koordinates, o u = u(x,y) - vaizdo intensyvumą tame taške. Vaizdo intensyvumas priklauso nuo trimatės vaizdo scenos objektų, apšvietimo, vaizdo stebėtojo pozicijos, plokščio vaizdo (2-atės projekcijos) registravimo būdo ir t.t.

Diskrečiu vaizdu vadiname analoginį vaizdą apibrėžiančios funkcijos imtis

u_i,j   =   u(x_i,y_j)

apibrėžtas diskrečioje gardelėje (x_i,y_j). Kaip taisyklė, imtys imamos vienodu atstumu x ir y kryptimis. Tokiu būdu, jei atstumą tarp gretimų taškų pažymėti h, gausime

u_i,j   =   u(ih,jh) .

Deja praktiškai gauti bet kokio analoginio signalo reikšmes taškuose (x_i,y_j) neįmanoma. Dalykas tas, kad bet koks šviesos intensyvumo matavimo prietaisas negali gauti intensyvumo tankio reikšmės idealiai lokalizuotame taške. Todėl kiekviena išmatuota reikšmė atspindi vidutinį intensyvumą taško (x_i,y_j) aplinkoje. Išmatuota intensyvumo reikšmė visuomet turi matavimo paklaidą. Dėl šios priežasties ir dėl to, kad kompiuteriuose galima saugoti tik baigtiniu skaičiumi bitų apibrėžiamą informaciją, išmatuota reikšmė yra kvantuojama.

Kvantuotos reikšmės yra numeruojamos ir numeriai sutapatinami su kvantuoto intensyvumo reikšme. Tokiu būdu gaunamas skaitmeninis vaizdas (signalas):

u_i,j   e   {0,1,...,M-1} .

Čia M žymi kvantų skaičių (tipiniu atveju M = 255).

Tačiau realiai mes suvokiame spalvotus vaizdus. Šis reiškinys yra gana sudėtingas. Šviesos intensyvumas yra tik integralinė patenkančio į matavimo pasirinktą plotą šviesos srauto energijos išraiška. Žvelgiant giliau, šviesos srautas sudarytas iš skirtingų dažnių elektromagnetinių bangų. Matematine prasme šviesos intensyvumas yra elektromagnetinių bangų galingumo pagal bangų dažnį integralas. Savo ruožtu neteisinga kalbėti apie taškinio signalo galingumo skleistinę pagal dažnius, nes taškinio šaltinio galingumas visiems bangos ilgiams yra vienodas. Problemos sprendimas analogiškas kalbos signalo atvejui - diskretizavimo taško aplinkoje vaizdo signalui pritaikoma lango funkcija ir kalbama apie "pasverto" lango funkcija vaizdo galingumo išdėstymą pagal dažnį.

Žmogaus rega sugeba dalinai išgauti informaciją apie šviesos srauto galingumo skleistinę pagal dažnius. Tiksliau, akies tinklainėje yra trijų rūšių kūgeliai specializuoti priimti artimas raudonos, žalios ir mėlynos spalvas atitinkančių dažnių šviesas. Regimos šviesos dažnių diapazonas yra nuo 360 iki 720 nanometrų.

Veidų išskyrimo metodikos

Išvardinsime populiariausias ir paprasčiausias veidų išskyrimo metodikas

1. Fono eliminavimas
   Jei veidas fotografuotas monochromatiniame fone, pakanka paprasčiausiai eliminuoti monochromatinį foną. Veidus taip pat nesunku išskirti, jei fotografuota statiniame (nekintame) žinomame fone.
2. Paieška pagal spalvą
   Pastebėta, kad veidų (žmogaus odos) spalvos išsidėsčiusios kompaktiškai. Tiksliau trimačiame spalvų kube yra kompaktiškos spalvų zonos, kurioms priklauso daugeliu atvejų veidą atitinkantys vaizdo taškeliai. Deja ši metodika jautri apšvietimo sąlygoms ir visiškai netinka pilkiems vaizdams.
3. Paieška pagal judesį
   Daugeliu atvejų video vaizdų scenose žmones atitinkantys objektai juda. Šiuo atveju pakanka taikyti bendras judesio sekimo technikas, kad aptikti vėliau veidą. Ši metodikai nelabai efektyvi, jei scenos yra sudėtingos ir juda daug objektų, arba priešingai - žmogus ilsisi ar miega.
4. Hibridiniai metodai
   Kadangi išvardinti metodai gana nepriklausomi, juos galima efektyviai kombinuoti. Jei kiekvieno metodo daromos klaidos ir teisingi atsakymai nepriklausomi, visuomet galima juos apjungti paprasčiausiai taikant kiekvieną metodą atskirai, kaupti rezultatų statistiką ir juos derinti.
5. Nespalvotų nejudančių veidų išskyrimas
   Šis atvejis yra sunkiausias, tačiau universalus, nes tinka ir kitais atvejais (spalvotiems, judantiems vaizdams).
   • Dirbtiniais neuroniniais tinklais pagrįsti metodai
   • Statistiniai klasterizavimo metodai
   • Veido modeliu pagrįsti metodai
   • Klasikiniai duomenys/požymiai/palyginimas su etalonais metodai

Violos ir Jones greitas veidų išskyrimo algoritmas

Trumpai aprašysime pora gerai pasiteisinusių veidų išskyrimo metodikų.

Pirmąją vadinsime jos autorių P. Viola ir M. J. Jones vardu. Šios metodikos pagrindinis privalumas - sparta. Viola ir Jones pasiūlė skaičiuoti labai paprastus ir greitai apskaičiuojamus parametrus. 1 paveikslėlis iliustruoja šių požymių keturis pagrindinius tipus. Paveikslėlio šablonai balta spalva žymi pozicijas, kuriose esantys vaizdo taškeliai sumuojami su pliuso ženklu, o pilka spalva žymi pozicijas, kuriose esantys taškeliai sumuojami ir paimami su minuso ženklu. Požymiu yra laikomas baltoje (-ose) ir pilkoje (-ose) srityje (-se) esančių taškelių skirtumas.

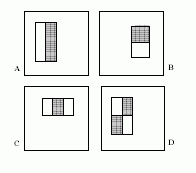
1 paveikslėlis. Keturi Haro tipo požymiai

Savo darbe Viola ir Jones naudojo 24x24 taškelių vaizdus, kuriuose galima priskaičiuoti iki 45396 Haro tipo požymių. Kad greitai apskaičiuoti požymio reikšmę, jie naudojo "kaupiamąjį vaizdą". 2 paveikslėlis iliustruoja jo reikšmę taške (x,y), kuri gaunama sumuojant vaizdo reikšmes pilkame stačiakampyje, kurio viršutinis kairysis taškas sutampa su vaizdo tuo pačiu kampiniu tašku, o apatinis dešinysis yra taške (x,y). Aišku, kad kaupiamąją sumą kompiuteryje galima efektyviai apskaičiuoti ir išsaugoti masyve, kurio matmenys bus tokie patys kaip ir pradinio vaizdo.

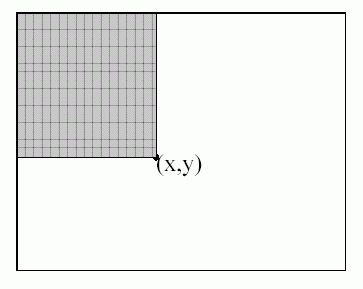
2 paveikslėlis. Kaupiamasis vaizdas taške (x,y) naudojamas greitai apskaičiuoti Haro tipo požymį.

Jei pažymėti kaupiamojo vaizdo reikšmes iu = iu(x,y) (i - žymi "Integral"), tai norint gauti vaizdo taškelių sumą stačiakampyje D su kampiniais taškais 1 ir 4 (žiūr. 3 paveikslėlį) pakaks keturių veiksmų: iu(4)+iu(1)-iu(2)-iu(3)

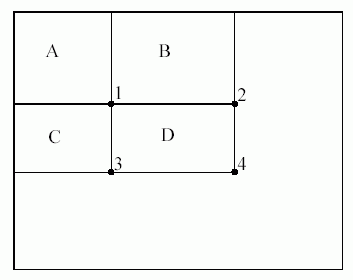
3 paveikslėlis. 1 ir 4 taškais apibrėžto stačiakampio D taškų suma iu(4)+iu(1)-iu(2)-iu(3)

Haro tipo požymiai bus apskaičiuojami analogiškai sudedant ir atimant atitinkamuose stačiakampiuose gautas reikšmes. Nežiūrint į greitą elementarių požymių apskaičiavimą vis viena naudoti visų požymių atpažinimui netikslinga. Kad išskirti geriausiai tinkamus klasifikacijai požymius, autoriai naudojo Adaboost apmokymo algoritmą. Šio algoritmo esmė yra tokia. Tarp didelio požymių parametrų aibės ieškomas nedidelis skaičius požymių, kurie sumuojami su svoriais ir duoda geriausius atpažinimo rezultatus. Kraštiniu atveju galite išrinkti vienintelį požymį, kuris kasifikuodamas pagal taisyklę:

h_j(x)   =   1   , jei p_jf_j(x) < p_jT_j,
h_j(x)   =   0   , priešingu atveju ,

darys mažiausiai klaidų. Čia x žymi 24x24 vaizdo fragmentą, f_j - j-ąjį požymį, T_j - klasifikavimo slenkstį, o p_j - ženklą. 4 paveikslėlis aprašo (anglų kalba) požymio, svorių ir klasifikavimo schemą naudojant AdaBoost metodiką. Pagal šią metodiką silpni h_j(x) yra apjungiami į vieną su svoriais. Čia T žymi naudojamų atpažinimui požymių skaičių.

4 paveikslėlis. T silpnų klasifikatorių paieškos ir apjungimo metodika.

Viola ir Jones atlikdami sistemos apmokymą eksperimentiniu būdu išskyrė 200 požymių (T=200), kuriuos naudodami gavo gerus atpažinimo rezultatus. 384x288 taškelių vaizdui apdoroti užtenka apie 1 sekundę. Šis greičio pasiekimas jų darbo paskelbimo metu buvo rekordinis. Aišku vien tik algoritmo greitis nieko nepasako, nes galima "labai greitai" su 1/2 tikimybe spėti, kad pateiktas 24x24 vaizdo fragmentas yra veidas arba ne.

5 paveikslėlis iliustruoja jų sistemos veidų išskyrimo kokybę. Abscisių ašyje atidedamos neteisingų teigiamų išskyrimų dažnis (vaizdo fragmentas buvo pripažintas veidu, nors iš tikrųjų toks nėra), o ordinačių ašyje - teisingai atpažintų veidų dalis. Pavyzdžiui išskiriant veidus 14084 testavimui skirtų vaizdų imtyje algoritmas darė vieną klaidingą teigiamą veido išskyrimą ir teisingai atpažino 95 procentus veidų. Trumpai objektų išskyrimo ir atpažinimo kreivės vadinamos ROC kreivėmis (angl. receiver operating curves). Kuo ROC kreive ribojamas plotas arčiau vieneto, tuo algoritmas geresnis. Taip pat svarbūs ROC kreivės ribiniai taškai, kurie atspindi kraštutinius atvejus - kokią dalį veidų algoritmas gali teisingai atpažinti nedarydamas nei vieno klaidingo teigiamo išskyrimo ir atvirkščiai - kokia bus dalis klaidingų teigiamų veidų išskyrimų išskiriant visus tikrus veidus teisingai. Sprendžiant iš grafiko, pirmasis skaičius yra apie 0.6.

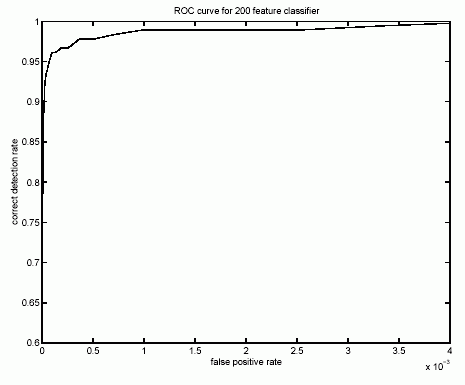
5 paveikslėlis. Neteisingų teigiamų / teisingai klasifikuotų veidų kreivė (taip vadinama ROC kreivė).

Algoritmo aprašymo pabaigai pateiksime AdaBoost algoritmu rastų pirmųjų dviejų požymių iliustraciją. Su šiais požymiais gaunama mažiausiai veidų išskyrimo klaidų (tiksliau gaunamas maksimalus ROC kreive ribojamos figūros plotas). Pastebėkime, kad kompiuteriu gautas rezultatas atitinka lūkesčius, kad atpažįstant veidus mes bene didžiausią dėmesį kreipiame į akis. Šį intuityviai suprantamą faktą paremia dar 1950-aisiais atlikti rusų psichofiziko Jarbus darbai (žiūr. 6, 7 paveikslėlius).

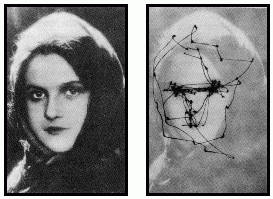6 paveikslėlis (kairiau). AdaBoost algoritmu surasti pirmieji du geriausią veidų išskyrimo rezultatą duodantys požymiai.

7 paveikslėlis (dešiniau). Žmogaus akių judesiais fiksuojamas dėmesys į stebimą moters paveikslą.

Hausdorfo metrikos panaudojimas išskirti veidams

Kitas pasiteisinęs veidų išskyrimo algoritmas remiasi Hausdorfo metrika. Hausdorfo metrika gerai tinka spręsti bendrus atpažinimo uždavinius.

1 apibrėžimas.

Tarkime A = {a₁, ... , a_m} ir B = {b₁, ... , b_n} yra dvi baigtinės tos pačios metrinės erdvės taškų aibės.
Tuomet Hausdorfo atstumu tarp A ir B aibių vadinamas dydis

H(A,B) = max {h(A,B), h(B,A)}

kur

h(A,B) = max_aeA min_beB ||a-b||

h(A,B) dydis vadinamas aibės A tiesioginiu Hausdorfo atstumu iki aibės B. ||a-b|| žymi atstumą tarp a ir b taškų. Vaizdų atveju pasiteisino kiek modifikuotas Hausdorfo tiesioginis atstumas apibrėžiamas išraiška

h(A,B) = 1/|A|S_aeA min_beB ||a-b||

Čia m = |A| žymi A aibės elementų skaičių.

Patogu A ir B aibėms suteikti tokią prasmę: A - atpažinimui skirtas vaizdas, B - objektas ieškomas vaizde. Iš Hausdorfo atstumo apibrėžimo aišku, kad tiesiogiai skaičiuoti Hausdorfo atstumą tarp vaizdo A ir objekto B nėra prasmės, nes jis praktiškai visuomet bus didelis. Todėl atliekami tokie žingsniai.

• Objektas B (etalonas) yra slenkamas
• Objektas B yra sukamas
• Keičiamas B mastelis
• Atlikus minėtas tris transformacijas iš vaizdo A iškerpama sritis atitinkanti transformuoto objekto B padėtį.

Turint vaizdą ir objektą/etaloną atliekamos transformacijos su įvairiais parametrais, kad minimizuoti Hausdorfo atstumą. Jei pažymėti galimų transformacijų aibę simboliu P, tai gausime tokią atstumo tarp A ir B formulę:

d_p^{^}(A,B) = min_peP H(A,T_p(B)) .

8 paveikslėlis iliustruoja aprašytą procedūrą grafiškai.

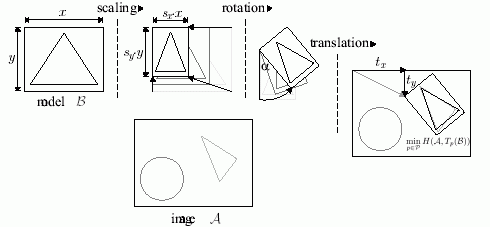
8 paveikslėlis. Objekto transformacijos minimizuoti Hausdorfo atstumą (šaltinis) Aišku, kad taikant tiesiogiai šią schemą pradiniams A ir B skaitmeniniams vaizdams gausime didžiulius skaičiavimo kiekius. Todėl atliekamas specifinis požymių išskyrimas A ir B vaizde, paliekantis tik mažą dalį charakteringų A ir B taškų. O. Jesorsky, K.J. Kirchberg, R.W. Frishholz darbe taškų mažinimo tikslu atliekami tokie pirminiai žingsniai.

• Taikant Sobelio operatorių išskiriami vaizde objektų kontūrai. Išskirti kontūrai binarizuojami naudojant adaptyvų slenkstį.
• Sudaromas objektui B charakteringų taškų šablonas.
• Pirminiame etape transformacijų parametras surandamas panaudojant modifikuotą Hausdorfo atstumą, o vėliau rasto optimalaus parametro reikšmė p^{^} yra patikslinama naudojant nemodifikuotą Hausdorfo atstumą.
• Galutiniame etape keičiamas modelis grįžtant prie vaizdų pateiktų pradine forma ir įvertinamas galutinis atstumas.

9 paveikslėlis iliustruoja visus veido išskyrimo remiantis Hausdorfo metrika etapus. Sprendžiant optimalios transformacijos paiešką galima naudoti genetinius minimizavimo algoritmus. Čia jų mes neaprašinėsime tačiau bendrais bruožais idėja yra tokia. Bet kokį globalaus minimumo paieškos uždavinį visuomet galima tiesioginio parametrų perrinkimo būdu, tačiau tai užima nerealiai daug kompiuterio resursų. Galima mažinti perrenkamų taškų skaičių atsitiktinai pasirenkant visas parametrų reikšmes, tačiau naudojant tokią strategiją galima gauti tolimas nuo globalaus minimumo reikšmes. Genetiniai minimizavimo algoritmai taupo ir skaičiavimų sąnaudas ir duoda neblogas minimumų reikšmes. Tai pasiekiama derinant atsitiktinį parametrų generavimą su perspektyvių parametrų rinkinių modifikavimu mėgdžiojant genetikoje stebimus procesus.

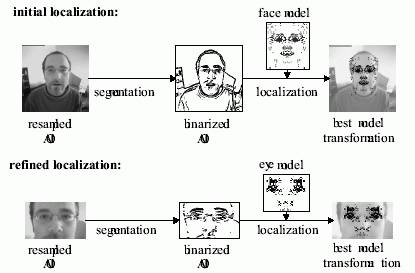
9 paveikslėlis. Veido išskyrimo etapai naudojant Hausdorfo metriką (šaltinis)

Nuorodos

Naudingos nuorodos parinktos pagal veidų išskyrimo specialistą Robert Frischholz

Nuoroda	Komentarai
Metodikos	Veidų išskyrimo populiariausių metodikų trumpi aprašymai
Straipsniai	Veidų išskyrimo rinktiniai straipsniai ir apžvalgos
Duomenys	Įvairios veidų atpažinimo ir išskyrimo algoritmų testavimo duomenų bazės
Programinė įranga	Nuorodos į laisvai platinimas ir komercines veidų išskyrimo bei atpažinimo sistemas
Nuorodos	Veidų išskyrimui skirtos nuorodos
Kita	Veidų iliuzijos ir kita

Praktinis darbas

Realizuokite veidų išskyrimo algoritmą Java kalba.
Jūsų sukurtas veidų išskyrimo algoritmas bus vertinamas pagal pateiktų algoritmui nežinomų veidų atpažinimo kokybę.

Reikalingų algoritmui atiderinti veidų pavyzdžius rasite čia arba galite pasirinkti čia.

---

Literatūra

1. Paul Viola and Michael J. Jones. Rapid Object Detection using a Boosted Cascade of Simple Features. IEEE CVPR, 2001
2. O. Jesorsky, K.J. Kirchberg, and R.W. Frishholz. Robust Face Detection Using the Hausdorff Distance. InProc. Third International Conference on Audio- and Video - based Biometric Person Authentication, Springer, Lecture Notes in Computer Science, LNCS-209ą, pp. 90-95, Halmstad, Sweden, 6-8 June 2001.
3. Rainer Lienhart, Alexander Kuranov, and Vadim Pisarevsky. Empirical Analysis of Detection Cascades of Boosted Classifiers for Rapid Object Detection. MRL Technical Report, Intel Labs, May 2002, revised Dec. 2002. [PDF]
4. Yoav Freud and Robert E. Schapire. A decision-thepretic generalization of online learning and an application boosting. In Computational Learning Theory: Eurocolt '95, pages 23-37. Springer-Verlang, 1995.
5. Akių judesiai stebint paveikslą
6. M.P. Dubuisson and A.K. Jain. A modified Hausdorf distance for object matching. In ICPR94, pages A:566-568, Jerusalem, Israel, 1994.
7. D.A. Forsyth slaidai. Templatematching

---

algirdas.bastys@maf.vu.lt

2005 m. vasario 23 d.