Automobilio numerio atpažinimas

1. Transporto srauto atpažinimo įrenginiai
2. Pirminis vaizdo apdorojimas
3. Automobilio numerio išskyrimas
4. Požymių išskyrimas
5. Numerio atpažinimas
6. Praktinis darbas
7. Literatūra

Transporto srauto atpažinimo įrenginiai

Šiuo metu Vilniaus mieste vis daugėja skaitmeninių vaizdo kamerų, kurios yra statomos pavojinguose kelių ruožuose ir sankryžose. Šios kameros perteikia eismo dalyvių vaizdus į punktą, kurio darbuotojai remiantis gaunama informacija priima sprendimus.

Tokia sistema taptų žymiai efektyvesne, jei būtų sukurta speciali programinė įranga, kuri sugebėtų patikimai atpažinti eismo dalyvių (automobilių) numerius. Turint tokią sistemą būtų galima automatizuoti vogtų ar neapdraustų automobilių paiešką.

Prieš aprašant skaitmeninio vaizdo kameromis grįstą sistemą, pateiksiu vaizdo kamerų sensorines alternatyvas.

1. Stacionarūs radarai.

   Kaip žinote radarai yra įrenginiai skirti įvertinti judančių objektų greitį. Šiuolaikiniuose radaruose įmontuojami skaitmeniniai fotoaparatai, kurie "dokumentuoja" (fotografuoja) greičio viršijimo faktą.

2. Mikrobanginiai detektoriai.

   Mikrobanginiai detektoriai dažniausiai montuojami ant tiltų nukreipiant mikrobangas į apačią automobilių srauto link. Judantis objektas atspindi mikrobangas kitu dažniu (priklausomai nuo objekto judėjimo greičio) ir tai leidžia skaitiniu būdu įvertinti jo judėjimo greitį.

3. Guminiai vamzdžiai.

   Guminiai vamzdžiai skirti registruoti srauto intensyvumą. Idėja labai paprasta. Guminis vamzdis pripildomas skysčio ir įmontuojamas į kelio dangą. Vienas jo galas aklinai uždaromas, o kitas sujungiamas su slėgio skaitmeniniu matuokliu. Autotransporto priemonės pervažiuodamos vamzdį laikinai padidina slėgį vamzdyje ir tai leidžiai patikimai ir paprastai užfiksuoti pravažiavusią transporto priemonę. Patiesus greta du guminius vamzdžius galima įvertinti ir judėjimo greitį, o atsižvelgiant į slėgio pokyčio dydį detektuoti priemonės tipą (pvz. langvasis automobilis, sunkvežimis).

4. Kilpiniai detektoriai .

   Šie detektoriai "gaudo" automobilius panašiai kaip tai daro kaubojai medžiodami mustangus prerijose. Po kelio danga yra patiesiamas kilpos formos laidininkas (viela). Pajungus įtampą abiejuose kilpos galuose susidaro uždara elektros grandinė, kuri jautriai reaguoja į induktyvumo kilpos viduje pokyčius. Patekę į kilpos plotą automobiliai dėl savo metalinių konstrukcijų keičia induktyvumą, kurio pokyčiai ir tampa judančių objektų detektavimo pagrindu. Jei ateityje pasirodys vien keramikiniai ar plastikiniai automobiliai, šis "mustangų gaudymo" prietaisas turės problemų.

Objektų atpažinimo prasme išvardintos skaitmeninių vaizdo kamerų alternatyvos yra žymiai paprastesnės, todėl detaliau jų nenagrinėsime.

Pirminis vaizdo apdorojimas

Šiame skyrelyje aprašysime automobilio numerio atpažinimo schemą.

1-2 paveikslėlis. Spalvotas automobilio vaizdas ir jo nespalvotas analogas

1 paveikslėlyje pateiktas skirtas numerio atpažinimui spalvotas vaizdas. Kadangi numerio atpažinimo uždavinio sprendimo kokybė neturėtų skirtis spalvinių ir nespalvinių duomenų atveju, tikslinga pradinį vaizdą konvertuoti į nespalvotą paveikslėlį. Tuo tikslu pakanka paprasčiausiai apskaičiuoti spalvos komponenčių aritmetinį vidurkį, t.y.

u_i,j = (R_i,j+G_i,j+B_i,j)/3,

arba (mėgstantiems tikslumą)

u_i,j = (299*R_i,j+587*G_i,j+114*B_i,j)/1000,

ir gautą nespalvotą paveikslėlį pateikti atpažinimui. 2 paveikslėlyje pateiktas tokios pirminės vaizdo apdorojimo procedūros darbo rezultatas.

Kyla klausimas kaip išryškinti gautame vaizde automobilio numerį. Vienas būdų galėtų būti išskirti vaizde kontūrus. Tuomet vaizde liktų tik intensyvumo greito kitimo linijos į kurias patektų ir numerio raidės bei skaitmenys. 3 paveikslėlyje pateiktas Sobel operatoriumi išskirti nespalvoto vaizdo kontūrai. Sobel operatorius aproksimuoja vaizdo gradientą, skaičiuodamas suvidurkintas dalines išvestines horizontalia ir vertikalia kryptimi. Formulių kalba gradientinis vaizdas s_i,j apskaičiuojamas pagal tokias formules:

s_i,j = SQRT((u_x_i,j)²+(u_y_i,j)²),

kur

u_x_i,j = ((u_i+1,j+1+2u_i+1,j+u_i+1,j-1)- (u_i-1,j+1+2u_i-1,j+u_i-1,j-1))/8;
u_y_i,j = ((u_i+1,j+1+2u_i,j+1+u_i-1,j+1)- (u_i+1,j-1+2u_i,j-1+u_i-1,j-1))/8 .

3-4 paveikslėlis. 2 paveikslėlio Sobelio operatoriumi išskirti kontūrai ir numerių išryškinimas taikant maxminmax žvaigždės tipo filtrą.

Gautame gradientiniame vaizde išryškėja mašinos numerio simbolių kontūrai. Kartu išryškėja ir visi kiti vaizdo kontūrai, t.y. tokios vietos vaizde, kuriose vyksta spartus intensyvumo kitimas.

Kyla klausimas ar negalima būtų rasti tokią operaciją, kur ryškintų numerio raidžių ir skaitmenų kontūrus ir neryškintų stambių sričių kontūrų. Norimą tikslą galima pasiekti "žvaigždutės" tipo netiesiniu "maxminmax" filtru. Šis netiesinis filtravimas atliekamas tokiu būdu:

1. Nurodytomis keturiomis kryptimis 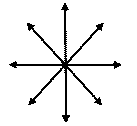ir pasirinkto ilgio atkarpose surandamos maksimalios vaizdo taškelių reikšmės. Slenkant krypčių šabloną per visą vaizdą gauname pirmą "max" tipo vaizdą.
2. Fiksuojame vaizdo taškelį u_i,j ir surandame minimumus iš žaliai ir mėlynai pažymėtų pirmame punkte rastų maksimalių reikšmių keturių trejetų, pavaizduotų šiame

   

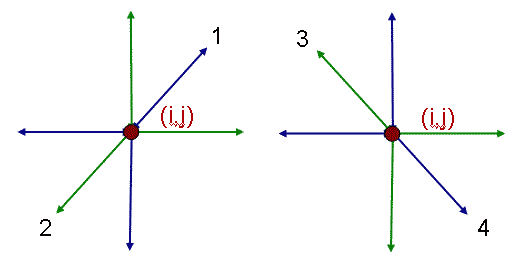
   paveikslėlyje. Slenkant per visus vaizdo taškelius suformuosime keturis "minmax" vaizdelius v^k-u, k=1,2,3,4.
   Čia u yra pradinis vaizdas.

3. Surandame "maxminmax" vaizdelį

   V_i,j = max_k v^k_i,j .

4. Kad pašalinti atsitiktinai dėl triukšmo išryškintas vaizdo detales surandame "maxminmax" vaizdo didžiausiąją reikšmę V_max ir suformuojame galutinį "maxminmax" vaizdą švelnaus slenksčio metodu pašalindami reikšme mažesnes už V_max/4, t.y.

   w_i,j = max{0,V_i,j-V_max/4} .

Slenksčio reikšmę V_max/4 fiksavome apibrėžtumo dėlei. Jei vaizdo numerio simbolių kontrastas yra nedidelis (fotografuojama rūko arba nakties sąlygomis ryškių automobilio šviesų fone), tokia slenksčio reikšmė gali būti per didelė ir ją reikėtų sumažinti. Čia susiduriame su tipine slenksčio reikšmės parinkimo problema. Kartais ją pavyksta išspręsti optimizuojant signalo/triukšmo santykį.

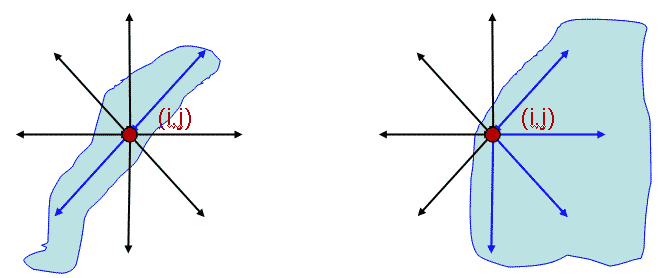
5-6 paveikslėlis. Neplačius tamsius vaizdo ruožus "maxminmax" žvaigždutės šablono filtras paryškina (kairysis paveikslėlis), o stambius blokus ir jų susidūrimus eliminuoja (dešinysis paveikslėlis).

5 paveikslėlis iliustruoja "maxminmax" netiesinio filtravimo poveikį neplačios vaizdo juostos primityvui. Paveikslėlyje išskirtame vaizdo taške (i,j) dviem iš šio taško išeinančiomis kryptimis (jos nuspalvintos mėlynai) gausime mažas maksimumų reikšmes, o likusiomis šešiomis (jos nuspalvintos juodai) gausime dideles maksimumų reikšmes. Todėl šiame taške (i,j), patenkančiame į siaurą juostą, atsiras bent vienas ketvertas, kurio visos trys šakos pasieks baltas vaizdo zonas, kuriose yra didelės intensyvumo reikšmės. Todėl trijų maksimumų minimumas bus pakankamai didelis, kad ženkliai viršyti vaizdo taškelio reikšmę u_i,j.

6 paveikslėlis iliustruoja "maxminmax" netiesinio filtravimo poveikį dviejų plačių vaizdo primityvų sandūroje. Šio paveikslėlio išskirtame vaizdo taške (i,j) keturiomis iš šio taško išeinančiomis kryptimis (jos nuspalvintos mėlynai) gausime mažas maksimumų reikšmes, o likusiomis keturiomis gausime dideles maksimumų reikšmes. Fiksuotas vaizdo taškas (i,j), patenka į tamsiąją sritį, visų krypčių ketvertų atveju bent viena iš trijų ketverto šakų papuls į tamsiąją vaizdo zoną, kur yra mažos taškelių intensyvumo reikšmės. Todėl trijų maksimumų minimumas bus mažas ir jis mažai skirsis nuo vaizdo taškelio reikšmės u_i,j.

Jei vaizdo taškelis (i,j) yra "baltojoje" zonoje, tai ir vienu ir kitu atveju formuojant "maxminmax" vaizdą bus atimama nemaža u_i,j ir todėl tokios vietos nebus paryškinamos.

Pritaikę aprašytą "maxminmax" netiesinio filtravimo procedūrą 2 paveikslėlio vaizdui gausime 4 paveikslėlyje pavaizduotą vaizdą. Iš šio vaizdo matome, kad numeris ryškiai išsiskyrė ir tokiame vaizde bus lengviau aptikti numerio vietą bei jį atpažinti.

Automobilio numerio išskyrimas

Nors po pirminio apdorojimo vaizdas supaprastėja, tačiau vis viena nėra aišku kurioje vaizdo dalyje yra mašinos numerį atitinkanti dalis. Vienas galimų problemos sprendimų būdų yra išskirti visas tamsias sritis ir taikyti joms raidės ar skaičiaus atpažinimo algoritmą. Lokalizuoti tamsiais sritis nesunku. Tuo tikslu galima binarizuoti pasirinktu slenksčiu vaizdą ir surasti gautame binarizuotame vaizde rišlias juodų taškų sritis.

7 paveikslėlis iliustruoja po binarizacijos gautą vaizdą, o 8-ame mėlynai pažymėtos ir sunumeruotos juodų taškų rišlios zonos. Kompiuteriu rišlias juodų taškų zonas galima gauti plintančios bangos metodu. Jo esmė yra paprasta:

1. Susirandame vaizde kokį nors juodai pažymėtą tašką;
2. Įtraukiame rastą tašką į naują juodų rišlių taškų sritį;
3. Iš rasto naujo taško paleidžiame "+" ("kryžiuko") šablono "bangą", įtraukdami į bangos frontą tuos kraštinius "kryžiuko" taškus, kurie atitinka juodus vaizdo taškus. Centrinį šablono tašką pažymime baltai;
4. Su kiekvienu bangos fronto tašku atliekame aprašytą procedūrą nuo pradžių;
5. Kai bangos frontas tampa tuščias, suteikiame rastų rišlių juodų taškų aibei identifikatorių ir pereiname prie naujo juodo taško vaizde paieškos. Jei naujų juodų taškų nėra, baigiame algoritmo darbą.

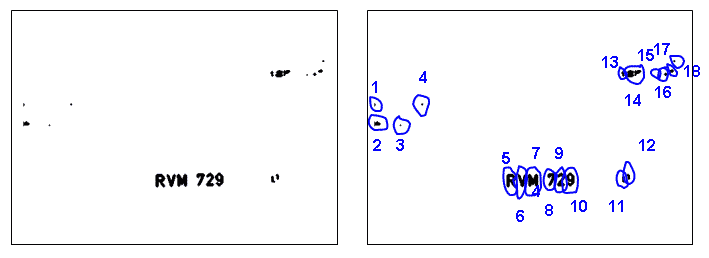
7-8 paveikslėlis. Binarizuotas "maxminmax" vaizdas su išskirtomis 18 rišlių tamsių taškų sričių.

Kyla klausimas kurios juodų taškų sritys atitinka raides arba skaitmenis, o kurios - ne. Kiekvienai tokiai sričiai galima būtų taikyti skaitmens arba raidės atpažinimo algoritmą, įvertinti atpažinimo tikėtinumą ir pasirinkus slenkstį priimti sprendimą apie juodų taškų zonos atitikimą skaitmeniui arba raidei.

Tačiau tokia atpažinimo strategija įvestų dar vieną sunkiai apibrėžiamą slenkstį. Remiantis apriorine informacija apie automobilio numerio struktūrą galime išvengti klaidoms jautraus pavienių sričių atpažinimo. Lietuviško standarto numerių atveju galime naudotis tokia apriorine informacija:

1. Numeris prasideda trimis vienodo mastelio raidėmis;
2. Numeris užsibaigia trimis to paties mastelio skaitmenimis;
3. Skaitmens ar raidės aukštis yra didesnis už plotį;
4. Viso gali būti 26+10 skirtingų simbolių, kurių skaitmeniniam užkodavimui reikia bent 6 langelių.

Kadangi realiomis sąlygomis autoeismo dalyvių nuotraukos gaunamos iš atokiai stovinčių vaizdo kamerų, tai numeris gali užimti tik mažą vaizdo dalį.

Naudojantis šia apriorine informacija galime atmesti sritis:

1. kurios yra mažos (8 pav. 1, 3-4, 13, 15-18 sritys);
2. kurios yra didelės (8 pav. tokių nėra)
3. kurių plotis didesnis už aukštį (8 pav. 2 ir 14 sritis)
4. kurios nesuformuoja panašaus aukščio bent trijų greta esančių grupės (8 pav. 11-12 ir kitos, išskyrus 5-7 + 8-9 trejetų grupes)

Tokiu būdu eliminavę iš 8 paveikslėlio netinkamas automobilio numerio raidėms ar skaitmenims sritis gausime 9 paveikslėlyje pavaizduotą rezultatą.

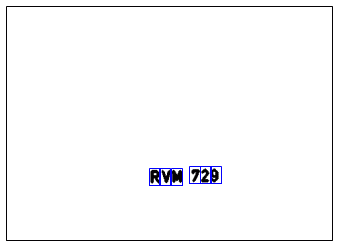
9 paveikslėlis. Binarizuotame vaizde išskirtos automobilio numerio raidžių ir skaitmenų sritys

Atkreipkite dėmesį, kad raidžių bei skaitmenų išskyrimo uždavinį išsprendėme visai nespręsdami individualių objektų (raidžių bei skaitmenų) atpažinimo uždavinio, o tik pasinaudodami bendra informacija apie šiuos simbolius.

Požymių išskyrimas

Prieš pereinant prie išskirtų simbolių atpažinimo reikia išskirti požymius, kurie ir yra pateikiami atpažinimui. Šiuo atveju turime binarizuotą vaizdą, jo mastelis nėra labai smulkus, todėl simbolio požymiais galime pasirinkti į fiksuotą langą patenkančias binarizuoto simbolio reikšmes. Pvz. jei fiksuoto lango dydis bus 18x28, tai atpažinimui pateikiamų požymių vektoriaus dimensija bus 504. Nors požymių dimensija yra didelė, tačiau kiekviena komponentė y_i turi tik dvi galimas reikšmes: 0 arba 1 ir tai supaprastina atpažinimą.

Galima atsisakyti požymių komponenčių binariškumo ir to dėka ženkliai sumažinti simbolio požymių vektoriaus dimensiją. [1] rekomenduojama suskaidyti fiksuoto lango taškelius suskaidyti į stambesnius blokus ir požymių vektoriaus komponente laikyti į stačiakampį patenkančių juodų taškelių skaičių arba dalį.
Pvz. jei 18x28 taškelius suskaidysime 3x4 stačiakampiais, tai nuo 504 binarinių požymių pereisime prie 42 požymių vektoriaus

Y = { y₀, y₁, ... , y₄₁ } .

Kiekviena požymio vektoriaus komponentė šiuo atveju turės 2¹² galimas skirtingas reikšmes. Kadangi galimų reikšmių yra pakankamai daug, galime laikyti, kad požymių vektoriaus Y komponentės yra skaičiai iš segmento [0,1], kurių prasmė - juodos spalvos dalis atitinkame 3x4 stačiakampyje. Taigi dabar vieno simbolio požymiai sudarytų 42 matavimų vienetinės aukštinės kubą. 10 paveikslėlis iliustruoja 6iuos požymių vektorius "R" ir "V" simbolių atveju.

Kyla klausimas ar pasirinkus aprašytą požymių sistemą mes sumažiname atpažinimui pateikiamos informacijos kiekį. Atsakymas į šį klausimą yra teigiama. Reikalas tame, kad perduodant tik į stambesnį stačiakampį patenkančių juodų taškelių dalį mes atsisakome informacijos apie konkrečias vietas, kuriose yra smulkūs juodi taškeliai. Mūsų konkretaus pavyzdžio atveju buvo galimi 2^18x28 skirtingi binariniai vaizdai ir 12^6x7 skirtingi 42 matavimų požymių vektoriai. Pastarasis skaičius yra ženkliai mažesnis:

12⁴²=2.1e+45 < 5.2e+151=2⁵⁰⁴ .

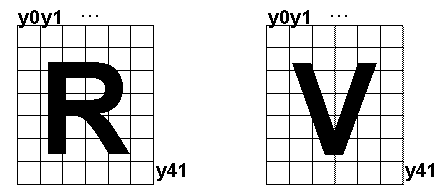
10 paveikslėlis. 42 simbolio požymiai apibrėžiami į 6x7 stačiakampius patenkančių vaizdo juodų taškelių dalimis.

[2] šaltinyje siūloma dar labiau sumažinti požymio vektoriaus dimensiją. Pagal siūlomą metodiką yra fiksuojami taškai ant išorinio stačiakampio, pasirenkamos kryptys ir požymiu apibrėžiamas atstumas nuo fiksuoto taško pasirinkta kryptimi iki binarizuoto vaizdo skeletono. Vaizdo skeletonas gaunamas ploninat juodų taškų juostas iki 1-etinio pločio juostų. Nors vizualiai nesunku įsivaizduoti kaip turėtų atrodyti konkretaus simbolio skeletonas, tačiau rasti algoritmą, kurio kompiuterinė realizacija gautų vizualiai laukiamus skeletonus nėra taip paprasta.

11 paveikslėlis iliustruoja 8-ų požymių sistemą, gaunamą ką tik aprašytu būdu, "R" ir "V" simbolių atveju. Šiuo atveju kiek kebliau įvertinti skaičių skirtingų galimų požymių, tačiau jis neturėtų viršyti

(7*6/2)⁴ = 194418 << 12⁴²=2.1e+45 < 5.2e+151=2⁵⁰⁴

skaičiaus. Gautas 8-ių komponenčių požymių skirtingų požymių vektorių skaičiaus įvertis yra nepalyginamai mažesnis už ankstesniuosius skaičius 42 ir 504 komponenčių požymių vektorių atveju, tačiau per daug džiaugtis nereikėtų. Reikalas tame, kad paprastindami požymių vektorių anksčiau ar vėliau susidursite su atveju, kai skirtingų simbolių vaizdai turės tuos pačius požymius ir tokiu atveju juos teisingai atpažinti iš jų požymių bus neįmanoma.

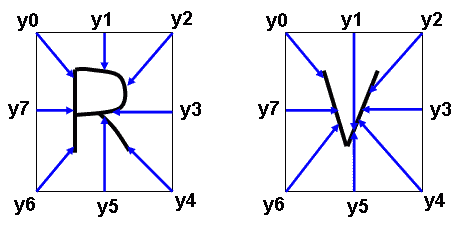
11 paveikslėlis. 8 simbolio požymiai apibrėžiami atstumais nuo fiksuotų 8 išorinio stačiakampio taškų iki binarizuoto vaizdo skeletono.

Trumpai aprašysime dar vieną požymių išskyrimo metodiką.

Vaizdo atpažinime natūralu reikalauti, kad jį aprašantys požymiai būtų invariantiški jo poslinkio, posūkio ir mastelio keitimo atžvilgiu.

Jei atpažįstamas simbolis teisingai išskirtas, nesunku suvienodinti tiriamojo ir etaloninio simbolio mastelį. Tuo tikslu galima pakeisti tiriamojo simbolio mastelį taip, kad jo aukštis sutaptų su etaloninių simbolių aukščiu. Tiesa, jei automobilio numeris stipriai pasisukęs horizonto linijos atžvilgiu, tiriamojo simbolio įvertintas aukštis gali neatitikti simbolio realaus aukščio. Šią problemą galima išspręsti atliekant pirma vaizdo posūkį taip, kad numerį sudarančius raides ir skaitmenis ribojantys stačiakampiai sudarytų lygiagrečią horizonto linijai seką.

Tiriamojo simbolio požymių invariantiškumo poslinkiui ir posūkiui problemą galima spręsti kartu tokiu būdu.

1. Apskaičiuojama išskirto simbolio autokoreliacinė funkcija:

   (uiu)_i,j = S_k,l u_k,lu_k+i,l+j

2. Apskaičiuojami rastos autokoreliacinės funkcijos sumos pasirinktuose žieduose:

   y_k = S_{i,j : (Rk)² ≤ i² + j² < (Rk+1)²} (uiu)_i,j.

Iš sekos y_k, k = 0, 1, ..., K-1, suformuosime požymių vektorių Y = ( y₀, y₁, ... , y_K-1 )^T. Žiedų spindulių R_k reikšmes reikėtų parinkti eksperimentiškai minimizuojant simbolių atpažinimo klaidų kiekį.

Autokoreliacinės funkcijos apibrėžimas garantuoja apibrėžto požymių vektoriaus invariantiškumą simbolio vaizdo poslinkiui, o sumavimas žiedais laiduoja požymių invariantiškumą vaizdo posūkiui.

Numerio atpažinimas

Kadangi numeris sudarytas iš atskirų raidžių ir skaitmenų, pakanka atpažinti kiekvieną atskirai išskirtą simbolį. Daugiametė spausdintinių simbolių kompiuterinio atpažinimo patirtis rodo, kad, jei simbolis išskirtas teisingai, tai daugelis atpažinimo metodikų gana patikimai atpažįsta išskirtus spausdintinius simbolius. Automobilio numerio atpažinimo atveju galime laikyti, kad pateikiami atpažinimui išskirti simboliai yra spausdintiniai. Taip yra dėl to, kad valstybiniai automobilių numeriai yra standartizuoti, jie gaminami ir skirstomi centralizuotai, ir tai lemia šio uždavinio panašumą į vieno šrifto spausdintinių simbolių atpažinimo uždavinį. Tačiau yra ir specifinių faktorių. Spausdintinių simbolių atpažinimo atveju skaitmeninis vaizdas gaunamas skenavimo būdu, o automobilio numeris yra fotografuojamas iš įvairių erdvės taškų, dėl ko tokiame vaizde atsiranda perspektyvinio pobūdžio iškraipymų.

Kai objektą aprašantys požymiai yra išskirti, tolimesnio atpažinimo metodikos praktiškai nepriklauso nuo pradinių duomenų specifikos. Kalbant simbolių terminas pradinis skaitmeninis vaizdas yra N=NXxNY skaičių u_i,j rinkinys, kuris paverčiamas K mačiu požymių vektoriumi

Y = ( y₀, y₁, ... , y_K-1 )^T .

Pasirenkant požymių vektoriaus apskaičiavimo taisykles labai svarbu išanalizuoti jų adekvatumą atpažįstamo objekto specifikai, tačiau tolimesniame atpažinimo etape, kuris remiasi išskirtais objekto požymiais, priklausomybė nuo pradinio objekto nėra ryški.

Todėl aprašant požymių vektoriais besiremiantį atpažinimą mes galime naudoti bendrus žymėjimus nekreipdami dėmesio į jų praktinę interpretaciją. Tarkime turime skirtų atpažinti L klasių

W₀, W₁, ... , W_L-1,

kurios kiekvienas konkretus atstovas w ∈ W_l yra N-matės erdvės R^N elementas atvaizduojamas į K-matį požymių vektorių

Y = ( y₀, y₁, ... , y_K-1 )^T .

Pažymėkime bendrą galimų požymių aibę simboliu D. Tuomet geometrijos požiūriu požymių vektorių atpažinimo arba klasifikavimo uždavinys ekvivalentus požymių erdvės D suskaidymui į poromis nesikertančius poerdvius D_l, l = 0,1,...,L-1, kurių kiekviena asocijuojama su to paties indekso objektų klase W_l. Mūsų sprendžiamo automobilio numerio atpažinimo uždavinio atveju skirtingų klasių skaičius L=36 (26 lotynų abėcėlės raidės ir 10 skaitmenų).

Trumpai apibūdinsime keletą atpažinimo metodikų.

Koreliacinė klasifikacija.

Viena paprasčiausių ir turinčių gana aiškią geometrinę interpretaciją yra koreliacinė klasifikavimo metodika. Paprasčiausiu atveju laikoma, kad požymių vektoriai yra K-matės euklidinės erdvės taškai, kurių panašumo lyginimui galima naudoti įprastą euklidinį atstumą. Tuo tikslu yra išsirenkami W_l klasių "etalonai" w_l ∈ W_l ir surandamas "panašiausias" etalonas į tiriamojo (atpažįstamo) simbolio požymio vektorių Y. Panašumui įvertinti naudojami koreliacijos koeficientai

c_l = <Y,w_l>/(|Y| |w_l|) .

Čia

<x,y> = S_0≤i<K x_i y_i ,
|x| = (<x,x>)^1/2 .

Suradus indeksą l_* su kuriuo koreliacijos koeficientas c_l* yra maksimalus, laikoma, kad šis požymio vektorius Y yra D_l* poerdvio elementas ir tokiu būdu paskelbiama, kad Y požymių vektorių atitinkantis elementas yra W_l* klasės atstovas.

Artimiausiojo kaimyno metodas.

Vienas aprašytos koreliacinės klasifikacijos trūkumų yra tai, kad panašumui apskaičiuoti naudojama euklidinė metrika, kuri laiko visas vektoriaus komponentes nepriklausomomis ir vienodo mastelio. Kitas trūkumas atsiranda dėl to, kad klasę apibūdina tik vienas etalonas. Pastarąjį trūkumą lengva pašalinti. Aprašysime praktiškai dažnai naudojamą artimiausiojo kaimyno klasifikatorių. Jis vietoje vieno klasės etalono naudoja visus duomenis, kuriems yra žinoma kokiai klasei jie priklauso ir yra vadinami apmokymo imtimi. Tuomet duotam požymių vektoriui surandamas jam artimiausias apmokymo imties elementas w_l*,i*, t.y.

|Y-w_l*,i*| = min_l,i|Y-w_l,i|

ir priimamas sprendimas, kad tiriamąjį požymių vektorių Y atitinka W_l* klasės atstovas.

Statistiniai ir neuroninių tinklų klasifikatoriai

Trumpai su kitais statistiniais ir kitais neuroninių tinklų tipo klasifikatoriais galite susipažinti čia [3].

Praktinis darbas

Sukurkite rašytinių skaitmenų atpažinimo algoritmą.
Jūsų algoritmas turi atlikti MNIST duomenų bazėje esančių skaitmenų atpažinimą pagal MNIST puslapyje aprašytą protokolą.
Algoritmas turi būti rašomas pratyboms skirtu laiku.
Darbo turi būti atliekamas ir atsiskaitoma atskirais etapais.
Bendra rašytinių skaitmenų atpažinimo algoritmo schema aprašyta čia, autorius Justas Janauskas.
Pirmieji laiku atlikę temas gali būti skatinami papildomais balais (iki 0.3).

1. Skaitmenų duomenų nuskaitymas ir pavaizdavimas paveikslėliu pateikiant jo žymę.
   Atsiskaitoma pademonstruojant keletą skaitmenų kompiuterio ekrane ir atspausdinant jų reikšmes.
   Vertinama 0.3 egzamino balo.
2. Skaitmenų binarizacija ir skeletono išskyrimas panaudojant vieną iš pateiktų skeletonizavimo algoritmų: K.Stukas, J.Janauskas, Š. Gruodis, M. Brašiškis.
   Atsiskaitoma pademonstruojant keletą skeletonizuotų skaitmenų kompiuterio ekrane.
   Vertinama 0.3 egzamino balo.
3. Skaitmens atvaizdavimas į fiksuoto dydžio stačiakampį ir jo pastorinimas pasirinktu spinduliu.
   Atsiskaitoma parodant standartinio dydžio pastorintą skaitmenį.
   Vertinama 0.9 balo.
4. Skaitmens binarinių požymių apskaičiavimas. Požymiams naudoti ypatingus skeletono taškus (pabaigos bei išsišakojimo) ir aštuonių sektorių aplinką.
   Atsiskaitoma parodant požymių apskaičiavimo metodą (funkciją), atspausdinus keletą reikšmių ir paaiškinant kodėl jos gavosi.
   Vertinama 0.5 balo.
5. Skaitmenų simetrinės panašumo metrikos realizacija ir skaitmenų palyginimas panaudojant panašumo metriką.
   Atsiskaitoma pademonstruojant gautas keleto skaitmenų porų panašumo įvertinimo reikšmes.
   Vertinama 0.7 balo.
6. MNIST testinių skaitmenų atpažinimas ir atpažinimo kokybės įvertinimas.
   Atsiskaitoma atlikus atpažinimo eksperimentus su testavimui skirtiems skaitmenims ir nurodant gautą atpažinimo kokybę - procentą teisingai atpažintų skaitmenų.
   Vertinama 0.7 balo.
7. MNIST testinių skaitmenų atpažinimo kokybės įvertinimas ROC kreive.
   Atsiskaitoma parodant ROC kreivę ir ją pakomentuojant.
   Vertinama 0.7 balo.

Semestro gale (iki gruodio 24 d. imtinai) galite pateikti savo sukurtą algoritmą konkursui, kurio rezultatai bus vertinami pagal pasiektą agoritmo kokybę. Kad dalyvauti konkurse, jūsų algoritmas turi būti pakankamai spartus: naudojant vieną giją 10000 MNIST testavimo pavyzdžiai turi būti sulyginami su 60000 MNIST mokymo pavyzdžiais ne ilgiau kaip per 6 val.

Reikalavimai programai.

1. Turite pateikti arba ".exe" arba "*.jar" komandine eilute paleidžiamą vykdomąjį failą.
   Komandines eilutes parametrai: mokymoPaveikliukai testavimoPaveiksliukai mokymoZymes testavimoZymes rocFailas.
   Naudojimo pvz:
   mano.exe mokymoDB testavimoDB mokymoLabels testavimoLabels Marytes.roc
   arba
   java -Xmx1024m -jar mano.jar mokymoDB testavimoDB mokymoLabels testavimoLabels Marytes.roc
2. Turi būti pateiktas išeities programų tekstų archyvas.
3. Pateikti algoritmai bus vertinami atskirai tokiose kategorijose:
   • EER
   • zeroFAR
   • ranking 1 procentas
   Kiekvienam studentui bus rasta geriausia tarp trijų kategorijų vieta ir rašomas toks egzamino kaupiamasis balas: 1-a vieta 5, 2-a 4, 3-a 3, 4-a 2. UŽ 5-ą ir žemesniai vietas skiriamas 1-as balas, jei pateiktas reikalvimus tenkinantis konkursui kodas.

Literatūra

1. Keinosuke Fukunaga. Introduction to statistical pattern recognition.
   Academic Press Professional, Inc. San Diego, CA, USA. 1980, 592 p.
   http://portal.acm.org/citation.cfm?id=92131
2. Fu K. Posliedovatielnyje metody v razpoznavanii obrazov i obucenii mashin.
   M. Nauka 1979
   (Russ.)
3. A. Bastys, Klasifikavimas, http://www.mif.vu.lt/~bastys/academic/ATE/Klasifikavimas/klasifik.htm
4. Vaizdų apdorojimo Java paketas
5. Parker&Ferdel

---

algirdas.bastys@maf.vu.lt

2004 m. spalio 11 d.