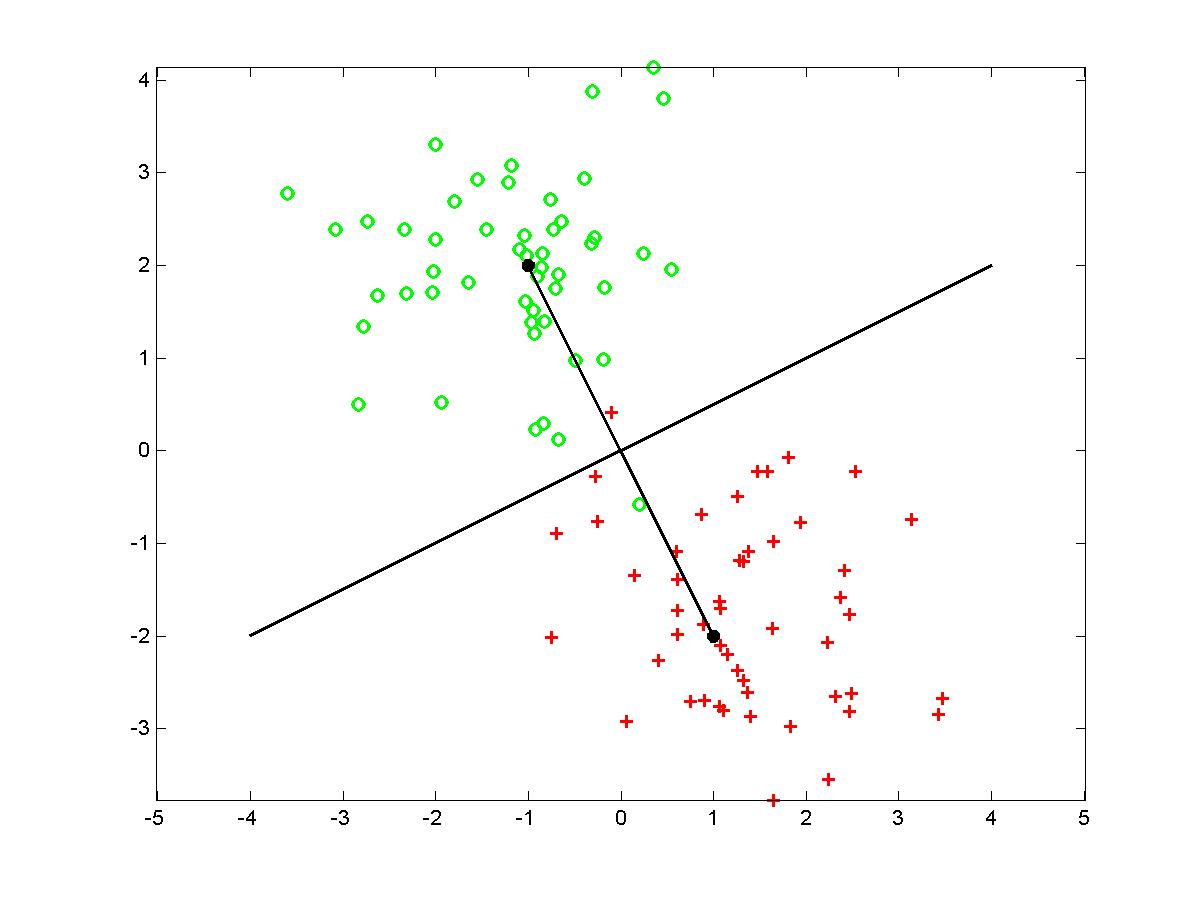
Dviejų grupių artimiausiojo vidurkio klasifikatorius.
Grupių centrai: M1 = (1,-2) ir M1 = (-1,2)
Klasifikacijos uždavinys yra specifinis atpažinimo uždavinys, kurio esmė pagal pateiktus objekto (vaizdo, proceso) skaitmeninius duomenis priskirti jį kokiai nors klasei. Laikysime, kad objektas yra aprašomas D-mačiu vektoriumi
SD= [ s1 , s2 , ... , sD ]' ,
o w1 , w2 , ... , wL
žymi visas klases, kurioms gali priklausyti objektas.
Čia ir toliau ' žymi transponavimo operaciją.
Klasifikacijos uždavinys yra sukurti duomenų žymėjimo
algoritmą. Matematine prasme klasifikatoriumi vadinamas bet
koks SD vektorių atvaizdis į L žymių
(kategorijų) aibę. Kadangi praktiškai žymių skaičius nebūna
labai didelis, dažniausiai yra apskaičiuojamos L funkcijų
reikšmės o1 , o2 , ... , oL ,
kurios yra interpretuojamos panašumo į atitinkamos kategorijos objektą
ir išsirenkamas indeksas su didžiausia panašumo reikšme.
Klasifikavimo uždavinys yra skaidomas į dvi dalis. Pirma yra surandamos objekto savybės (angl. features). Pažymėkime objekto savybių skaičių n. Savybės yra apskaičiuojamos remiantis pradiniu objektą aprašančiu vektoriumi SD. Parenkant objekto savybes yra ieškoma kompromiso tarp
Antrajame etape remiantis požymių vektoriumi
X= [ x1 , x2 , ... , xn ]'
yra atliekama klasifikacija.
1 pvz. Tarkime SD= [ s1 , s2 , ... , sD ]' žymi stacionaraus akustinio signalo garso slėgio reikšmes. Tuomet geru požymių rinkiniu yra SD duomenų tiesinės prognozės koeficientai X= [ x1 , x2 , ... , xn ]' .
Toliau paprastumo dėlei laikysime, kad yra tik dvi kategorijos, t.y., L=2. Tai nėra esminis apribojimas, kadangi pradžioje gali apjungti visas kategorijas į dvi grupes. Atlikę pirmąją klasifikaciją, rasime kuriai grupei priklauso tiriamas objektas. Toliau rasta grupė skirstoma vėl į dvi dalis, atliekama klasifikacija, kad surasti kuriam pogrupiui priklauso objektas ir t.t.
Kad sukurti klasifikatorių, pradžioje yra pasirenkama aibė duomenų vektorių SD su žinomom kategorijų reikšmėm. Ši aibė yra pagrindas kuriant klasifikatorių. Kadangi iš pradinių duomenų galima išskirti įvairius požymių rinkinius, dažnai neapsiribojama vienu klasifikatoriumi, o kuriama skirtingiems rinkiniams skirtingi klasifikatoriai. Taip natūraliai iškyla klausimas - kuris klasifikavimo algoritmas yra geriausias? Todėl bendra pradinių duomenų grupė skaidoma į dvi dalis
Yra naudojamos įvairios strategijos kuriant ir įvertinant klasifikavimo algoritmus. Dažnai apmokymo ir verifikacijos imtys yra sukeičiamos vietom ir žiūrima kaip keičiasi rezultatai. Taip pat naudinga turėti dar vieną klasifikuotų duomenų grupę, kuri naudojama tikrinti algoritmus tik vieną kartą. Taip išvengiama algoritmo adaptacijos prie turimų duomenų. Vieną kartą naudojam tikrinimo imtis vadinama testine.
Dažnai laikoma, kad požymiai X yra pasiskirstę pagal kokį nors daugiamatį skirstinį. Tokia matematinė abstrakcija suteikia galimybę įvertinti klasifikavimo algoritmą vienareikšmiais skaičiais, kurie gaunami naudojant statistikinę informaciją apie populiaciją. Šiuo atveju geru požymiu dažnai yra skirtingų kategorijų požymių vidurkiai M1 , M2 , ... , ML .
Konkretaus požymių vektoriaus X euklidiniai atstumai iki kategorijų vidurkių, kurių kvadratai apskaičiuojami pagal formules
||X-Ml||2 = ( X-Ml )'( X-Ml ),
yra vienas galimų panašumo į kategorijas matų. Tokių atstumų pagrindu atlikta klasifikacija vadinama euklidinio atstumo klasifikatoriumi (angl. Euclidean distance clasifier EDC). Kartais EDC dar vadinami artimiausiojo vidurkio klasifikatoriumi.
Dvi pirmąsias kategorijas skirianti riba randama iš lygybės
||X-M1||2 - ||X-M2||2 = 0.
Nesunku pastebėti, kad ši riba X atžvilgiu yra tiesinė. Taigi arčiausiojo vidurkio dviejų kategorijų klasifikatorius apibrėžiamas tiesine diskriminantine funkcija
h(X) = X' V + c,
kur
V = M1 - M2 ir c = - (M1 + M2 ) ' V / 2.
Klasifikavimas atliekamas pagal diskriminantinės funkcijos ženklą - jei jis yra '+', tai X požymius atitinkantis vektorius priskiriamas 1-ai klasei, priešingu atveju - 2-ai klasei. Žemiau pateikta iliustracija dviejų grupių klasifikavimas naudojant artimiausiojo vidurkio metodą.

Paprastas euklidinio atstumo pagrindu sukurtas klasifikatorius yra asimptotiškai (kai apmokymo duomenų skaičius artėja į begalybę) optimalus, jei duomenys pasiskirstę pagal sferinį Gauso dėsnį NX(Ml , s2I). Čia I žymi vienetinę matricą, o s2 I - kovariacijos matricą.
Jei požymių kovariacinė matrica S nėra įstrižaininė, klasifikavimas pagal artimiausiąjį kategorijų vidurkį nėra optimalus. Šiuo atveju geriau tinka Fišerio dar 1936 m. pasiūlytas klasifikatorius.
2 pvz. Žemiau pateiktame pavyzdyje palygintos klasifikavimo tiesės gautos taikant Euklidinį atstumą (E) ir Fišerio metodą. Naudojant klasifikavimui pateiktus N1 ir N2 duomenis, tiesinio klasifikavimo taisyklė h(X) = X' VF + c, gaunama tokiu būdu:
VF = S-1 (M1 - M2) ir c = - (M1 + M2 ) ' VF / 2,
o empirinė kovariacijos matrica apskaičiuojama pagal formulę
S = 1/(N1 + N2 - 2) Si=12 Sj=1Ni ( Xji - Mi ) ( Xji - Mi )'.
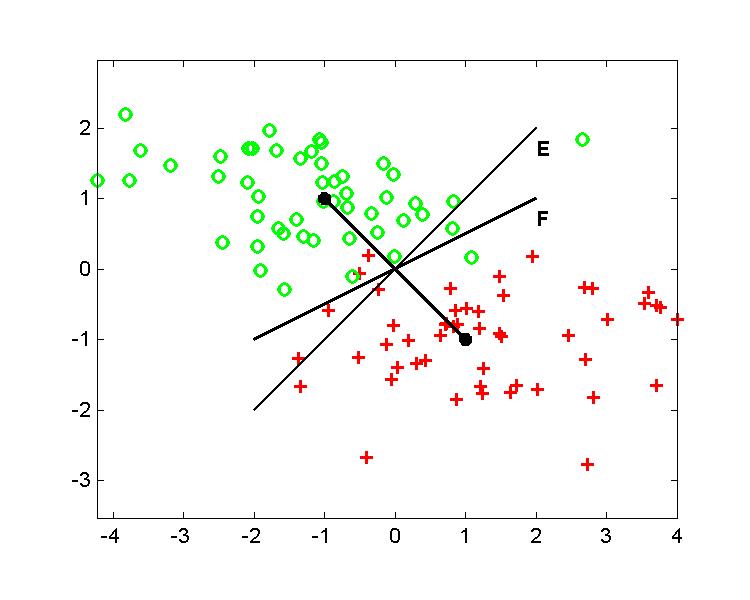
Jei grupių požymių vektoriai pasiskirstę pagal daugiamatį Gauso dėsnį su ta pačia kovariacine matrica ir skirtingais vidurkiais, tai standartinis Fišerio klasifikatorius yra optimalus. Naudojant vektorių VF ir konstantą c Fišerio tiesinis klasifikatorius išreiškiamas formule
h(X) = X' VF + c.
Ir vienu ir kitu atveju išvesdami klasifikavimo taisyklę mes darėme prielaidą apie duomenų pasiskirstymą, įvertindavome pasiskirstymo parametrus ir po to gaudavome klasifikavimo taisyklę. Silpna vieta čia yra daroma prielaida apie parametrinį pasiskirstymo dėsnį. Daugelis autorių teigia, kad vietoje prielaidos apie pasiskirstymo dėsnį geriau fiksuoti kokiai klasei turi priklausyti klasifikavimo taisyklė ir toje klasėje ieškoti optimaliai atskiriančio grupes klasifikatoriaus. Pavyzdžiui, galima fiksuoti, kad mūsų klasifikatoriaus funkcija tiesiškai priklausys nuo požymių vektoriaus ir tarpe visų tiesinių išraiškų ieškosime skiriamosios tiesės geriausiai skiriančios apmokymo duomenimis. Panašios klasifikavimo paradigmos laikosi dirbtinių neuroninių tinklų pagrindu sukurti klasifikatoriai.
Susipažinsime su MEE (angl. minimum empirical error) klasifikatoriumi, kuris priklauso tiesinių klasifikatorių aibei ir randamas tiesiogiai minimizuojant klasifikavimo paklaidą.
3 pvz. Žemiau pateiktame brėžinyje palygintos klasifikavimo tiesės gautos taikant Euklidinį atstumą (E), Fišerio (F) ir minimalios empirinės paklaidos (MEE) metodą. Klasifikavimui pateiktos dvi plokštumos taškų grupės, kurios skiriasi vidurkiais: M1 = -M2 = 0.5. Prie abiejų grupių taškai pasiskirstę pagal normalųjį dėsnį su ta pačia kovariacine matrica, kurios kvadratinės formos vieną lygio liniją iliustruoja elipsė.
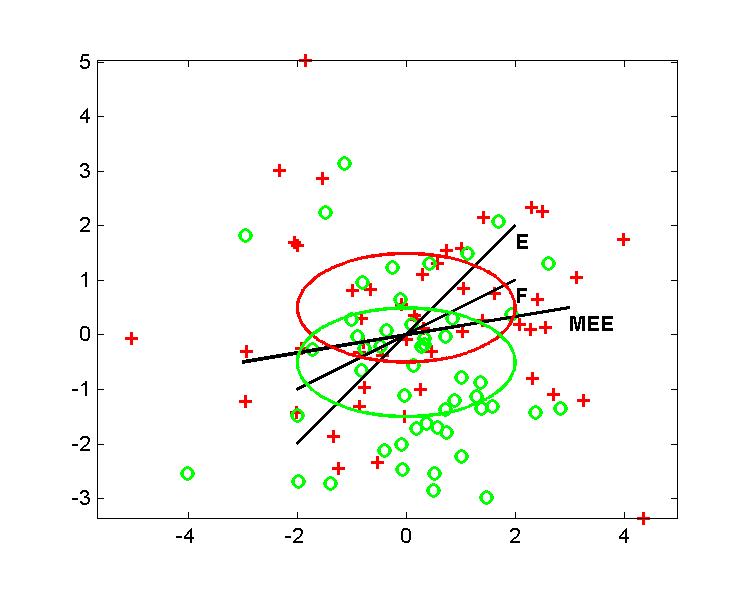
Iš brėžinio matyti, kad tiesiogiai duomenų imčiai adaptuotas
tiesinis klasifikatorius (MEE) geriausiai atlieka skirtingų grupių
taškų atpažinimą. Tačiau nebūtinai šis klasifikatorius yra
geriausias. Neuroniniuose tinkluose susiduriama su reiškiniu,
vadinamu tinklo pertreniravimu (angl. overtraining.
Jo esmė yra per didelė parametrų adaptacija prie pateiktos duomenų
specifikos. Pertreniravimas reiškia, kad tinklo mokymo
eigoje buvo pereitas etapas, kuriame einamosios parametrų reikšmės
būtų davusios geresnius verifikacinius rezultatus.
Vienasluoksniai ir daugiasluoksniai perceptronai
Paprastasis perceptronas
yra paprasčiausias gyvo organizmo neurono matematinis modelis.
Vienasluoksnis perceptronas yra grupė paprastųjų perceptronų, naudojančių bendrą požymių vektorių. Pas žmogų yra milijardai tarpusavyje sujungtų neuronų. Laikoma, kad gyvuose organizmuose neuronai grupuojasi sluoksniais, o šie savo ruožtu taip pat jungiasi tarpusavyje. Taip susidaro sudėtinga struktūra skirta apdoroti informacijai. Tuo atveju kai sluoksninė neuronų struktūra yra imituojama jos matematiniu modeliu, kompiuteriu ar elektrinėm schemom, vartojamas dirbtinių neuroninių tinklų terminas (angl. Artifical Neural Networks (ANN) ).
Paprastasis perceptronas sudarytas iš
o = f ( V'X + c ).
Dirbtiniuose neuroniniuose tinkluose perceptronų perdavimo funkcijos yra vienodos ir vienas nuo kito perceptronai skiriasi tik svorių V' = w1, w2, ... , wp ir poslinkio c reikšmėm. Klasikiniu atveju perdavimo funkcija yra sigmoidinė, t.y.,
f(x) = 1/(1+e-x).
Paprastasis perceptronas yra specifinės struktūros diskriminantinė funkcija, x1, x2, ... , xn yra požymiai, o o svoriai ir poslinkis apibrėžia konkrečią diskriminantinės funkcijos išraišką.
Net vienu perceptronu galima atlikti požymių vektoriaus X klasifikaciją. Kadangi perdavimo funkcija turi tik dvi stabilias reikšmes - 0 ir 1, klasifikavimo kategorijų (grupių) skaičius lygus 2, o sprendimo taisyklė yra tokia: jei o viršija slenkstinę reikšmę 0.5, X priskiriamas vienai grupei, priešingu atveju - kitai. Iš čia ir f argumento išraiškos V'X + c gauname, kad perceptrono sprendimo skiriamoji riba yra tiesinė. Perceptrono svoriai surandami minimizuojant baudos funkciją apibrėžtą apmokymo aibėje. Paprasčiausia ir populiariausia yra kvadratinė baudos funkcija: bauda = 1/(N1+N2) Si=12 Sj=1Ni ( tji - f ( V'Xji + c ) ) 2,
kur tji yra tikslo reikšmė duotajam mokymo požymių vektoriui Xji . Mūsų atveju galima pasirinkti tj1 = 1 , tj2 = 0 arba tj1 = 0.95 , tj2 = 0.05 . Bendru atveju pasirenkamos tikslo reikšmės turi tenkinti nelygybę 0 < tji <1 .
Aprašytas perceptronas kiek pasikeistų, jei būtų naudojama kita populiari perdavimo funkcijos išraiška
f tanh(x) = ( ex - e-x ) / ( ex + e-x ) = 2f sigmoid(2x) - 1.
Šiuo atveju geriau būtų tj1 = 1 , tj2 = -1.
Slenkstinei perdavimo funkcijai
f hard(x) = 1 kai x > 0 , f hard(x) = 0 kai x < 0
vėl tinka tj1 = 1 , tj2 = 0.
Klasikiniu atveju perceptrono svoriai randami gradientiniu metodu minimizuojant baudos funkciją. Tuo tikslu skaičiuojamos baudos funkcijos dalinės išvestinės atžvilgiu ieškomų parametrų ir svoriai keičiami tokiu iteraciniu būdu:
Vt+1 = Vt - h baudaV', ct+1 = ct - h baudac'.
Čia baudos išvestinė atžvilgiu vektoriaus žymi gradientą.
Slenksčio funkcijai šis gradientinis metodas netinka. Kad pradėti iteracinį
procesą, reikia apibrėžti pradinius svorius V0
ir laisvąjį narį c0. Literatūroje
rekomenduojama pradines svorių reikšmes imti nedidelius atsitiktinius skaičius.
Mes kiek vėliau susipažinsime su trim skirtingais pradinių svorių
parinkimo variantais, su kuriais galima gauti visus tris anksčiau
nagrinėtus tiesinius klasifikatorius.
Grupė parastųjų perceptronų, naudojanti tuos pačius įvesties parametrus,
sudaro vienasluoksnį perceptroną. Kelių vienasluoksnių
perceptronų struktūra vadinama daugiasluoksniu perceptronu arba
dirbtiniu neuroniniu tinklu. Daugiasluoksnio perceptrono įvestį sudaro
požymių vektoriaus X = ( x1 , x2 , ...
, xn )' komponentės
x1 , ... , xn. Vieno sluoksnio perceptrono
išėjimai (angl. output) sudaro kito sluoksnio įėjimą
(angl. input). Perceptronų sluoksniai tarp įėjimo ir paskutinio
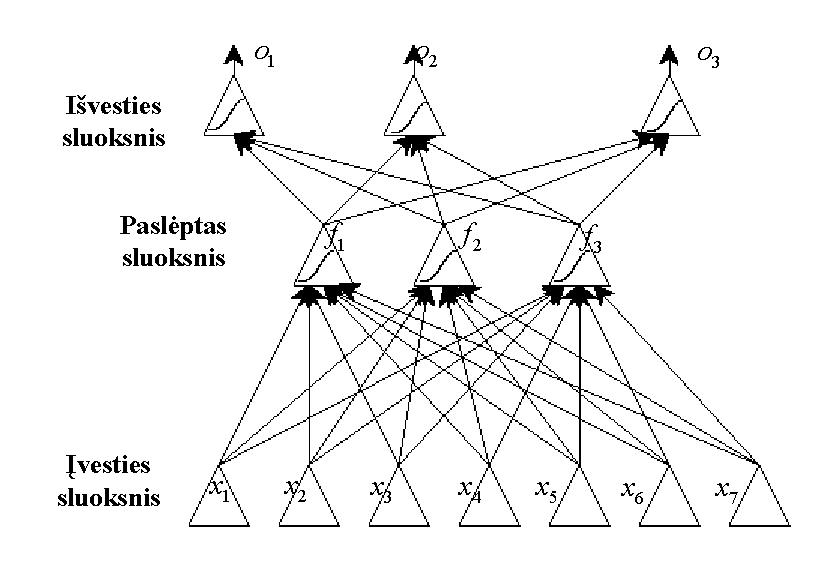
vadinami paslėptais (angl. hidden). Pateiktas brėžinys
iliustruoja dvisluoksnį perceptroną su vienu paslėptuoju sluoksniu,
požymių vektorius yra septinmatis, paslėptąjį sluoksnį sudaro trys perceptronai,
išvesties (antrąjį) sluoksnį taip pat trys perceptronai.
Paskutiniojo sluoksnio perceptronai naudojami skirtingom klasėm žymėti.
Tipiniu atveju paskutinio sluoksnio perceptronų skaičius yra lygus
skaičiui skirtingų klasių (kategorijų), kurias reikia atpažinti. Tarkime,
jei reikėtų atpažinti skaitmenis, tai atpažinimui tikslinga būtų pasirinkti
daugiasluoksnį perceptroną, turintį 10 išeities perceptronų.
Daugiasluoksnio perceptrono svoriai taip pat surandami iteraciniu
būdu minimizuojant baudos funkciją. Kadangi paslėptųjų sluoksnių
perceptronams tiesiogiai nėra kaip parinkti tikslo reikšmes, skaičiuojant
gradientą atsiranda tam tikros rekurencijos,
vadinamos
tji - f ( V'Xji + c )
paklaidų atgaliniu sklidimu (angl. Back Propagation).
Naudojant slenkstines funkcijas požymių plokštumoje
grupes skiriančios ribos sudaro laužtę (laužtė - tolydi kreivė
sudaryta iš tiesės atkarpų). Jei perdavimo funkcija f
yra diferencijuojama, skiriamoji riba neturi aštrių kampų.
Bendru atveju dvisluoksniu perceptronu su vienu paslėptu
sluoksniu naudojant pakankamai daug perceptronų
galima gauti kiek norima sudėtingą dvi grupes skiriančią ribą.
Esminio skirtumo tarp naudojamų perdavimo funkcijų nėra.
Pavyzdžiui, pasirenkant mastelį galima pasiekti, kad
sigmoidinė perdavimo funkcija duotų skiriamąsias
ribas panašias į ribas gaunamas su slenksčio funkcija.
Paprastumo dėlei tarkime,
kad yra tik dvi grupės (kategorijos),
abiejų grupių apmokymo imtys yra vienodo dydžio
(N1 = N2 = N = N/2) ir duomenys
yra centruoti, t.y.,
bauda = 1/N
Si=12
Sj=1N
( tji - ( V'Xji + c ) ) 2
su simetrinėm tikslo reikšmėm
tj1 = 1 ir
tj2 = -1 .
Parodysime, kad prie šių sąlygų startuojant nuo nulinių svorių
V0 = 0 ir nulinės poslinkio konstantos
c0 = 0 jau po pirmojo gradientinio vieno perceptrono
treniravimo žingsnio gauname naują svorio vektorių ir poslinkio konstantą,
su kuriais apskaičiuojamas perdavimo funkcijos argumentas daugiklio
tikslumu sutampa su artimiausiojo vidurkio (euklidinio atstumo) metode
naudojama klasifikavimui išraiška.
Apskaičiavę baudos funkcijos išvestinę atžvilgiu kintamojo
c ir gradientą atžvilgiu svorio vektoriaus V, gausime
d bauda / dc = -2/N
Si=12
Sj=1N
( tji - ( V'Xji + c ) ) =
2 c + 2 V' M,
d bauda / dV = -2/N
Si=12
Sj=1N
Xji ( tji - ( (Xji)' V + c ) ) =
-D M + 2 K V,
kur
D M = M1 - M2
ir
2 K V = 1/N
Si=12
Sj=1N
Xji ( Xji )'.
Įstatę šiose formulėse pradines nulines svorių ir poslinkio reikšmes,
gauname tokias atnaujintas po pirmosios iteracijos reikšmes:
V1 = V0 -
h d bauda / d V =
h D M ,
c1 = c0 - 0 = 0.
h baudac'.
Taigi daugiklio tikslumu išraiškos naudojamos klasifikuoti
arčiausiojo vidurkio ir perceptrono, gaunamos po pirmosios iteracijos,
yra vienodos. Kadangi klasifikuojama pagal diskriminantinės funkcijos
ženklą, tai daugiklis nekeičia klasifikavimo rezultatų.
Taigi, jei
Fišerio klasifikatorius gaunamas minimizuojant
baudos funkciją antrosios eilės metodu. Prilyginę baudos funkcijos
gradientą nuliniam vektoriui, randame svorio vektoriaus išraišką
V = 1/2 K-1 DM.
Centruotiems duomenims (M = 0) matricą K
galime išreikšti
K = (N-1)/N S
+ 1/4DM
DM',
S = 1/(N1 + N2 - 2)
Si=12
Sj=1Ni
( Xji - Mi )
( Xji - Mi )'.
Naudodami Bartleto teigiamos simetrinės matricos apgrąžos formulę
(A + VV')-1 =
A-1 - ( A-1VV'A-1 ) /
( 1 + V'A-1V ) ,
svorio vektorių išreikšime
V = k S-1DM,
kur k = 2 / ( D2 + 4(N-1)/N ) ir
D2 = DM'
S-1 DM . Taigi vėl iš paprasto perceptrono vienu antrosios eilės baudos
minimizavimo būdu gauta svorio išraiška duoda daugiklio
tikslumu tą pačią išraišką kaip ir Fišerio tiesinis klasifikatorius.
Dviejų sluoksnių perceptronas.
Apie atgalinio sklidimo algoritmą, skirtą daugiasluoksnių
perceptronų mokymui, galite paskaityti
http://scitec.uwichill.edu.bb/cmp/online/p21h/Lecture9/lect9.htm.
Dviejų sluoksnių perceptronų skiriamosios ribos.
Punktyrinė linija - naudojama slenkstinė perdavimo funkcija,
ištisinė kreivė - glodi perdavimo funkcija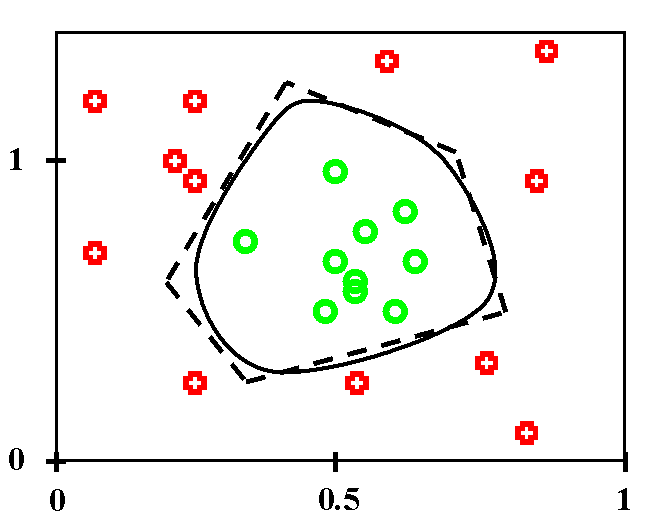
Ryšys tarp paprastojo perceptrono ir euklidinio ir Fišerio klasifikatorių
Parodysime, kad tam tikra prasme euklidinis ir Fišerio tiesinis klasifikatoriai
yra atskiras paprastojo perceptrono atvejis.
M = ( M1 + M2 ) / 2 = 0.
Toliau laikysime, kad perdavimo funkcija yra tiesė
f(x) = x , baudos funkcija apibrėžiama
Aprašytas rezultatas teisingas bet kokiai nelyginiai diferencijuojamai
perdavimo funkcijai.
Literatūra