Krypčių lauko ir orientacijos apibrėžimai

Matematiškai krypčių laukas apibrėžiamas diferencialine lygtimi

dy/dx = g(x,y) .

Bet kokiame plokštumos taške (x,y) kryptis apibrėžiama vienetinio ilgio vektoriumi

{ 1 / (1 + g²(x,y))^1/2 , g(x,y) / (1 + g²(x,y))^1/2 }

Vaizdams šis apibrėžimas nelabai tinka. Jei plokštumoje apibrėžto analoginio vaizdo intensyvumo pilkumo lygmenis pažymėti funkcija f = f(x,y) , tai orientacijų lauku arba tiesiog orientacijomis vadinsime tiesių pluoštą, kur kiekviena pluošto tiesė apibrėžiama taško (x₀,y₀) koordinatėmis taip, kad tiesė kerta tašką (x₀,y₀) ir f(x,y) = f(x₀,y₀) lygio liniją.

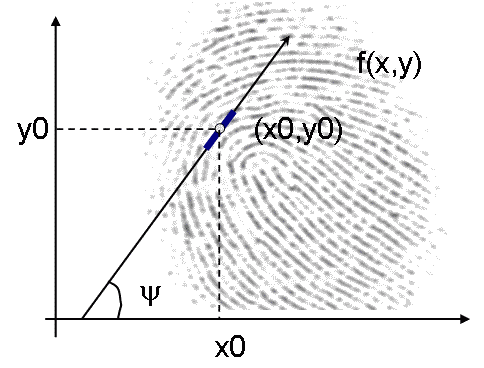
1 paveikslėlis. Vaizdo orientacija taške (x₀,y₀)

Kryties vektorius apibrėžiamas kampu, kuris kinta nuo 0 iki 2p, o orientacija kampu, kurį sudaro liestinė su x ašimi. Orientacijos kampas y kinta nuo 0 iki p. Egzistuoja paprastas sąryšis tarp funkcijų g ir f, kurios apibrėžia krypčių ir orientacijų laukus:

g(x,y) = - (df/dx)/(df/dy) .

Todėl kampas, kuriuo kerta liestinė ašį x tenkina lygybę

tgy(x,y) = - (df/dx)/(df/dy), 0 ≤ y <p.

Taikymai

Orientacijų laukas yra taikomas:

• Vaizdų, kuriuose yra beveik periodinės struktūros, kompresijai.
• Atpažinime. Pavyzdžiui atpažįstant pirštų antspaudus, tekstūras, interferencinius, kristalų vaizdus.
• Kompiuterinėje geometrijoje.
• Diferencialinių lygčių sprendime ir sprendinių tyrime.
• Duomenų vizualizacijoje.

Kokiu atveju tikslinga taikyti krypčių ir orientacijos laukus ? Bendra taisyklė yra tokia - jei vaizde yra pasikartojančios struktūros, tai jas galima ekonomiškai charakterizuoti savotiška koordinačių sistema, kurios viena ašis skirta vaizduoti pasikartojamumo periodą, o kita ašis - kryptį, kuria vyksta pasikartojimas. Palyginkime piršto antspaudo ir jo Furjė spektrinio tankio vaizdus. Pirmasis nėra sudėtingas, jame, kaip ir bet kokiame piršto antspaudo vaizde matyti beveik periodiškas atsikartojimas, tačiau atsikartojimo kryptys yra įvairios. Orientacijų ar krypčių laukas perteikia informaciją apie šias atsikartojimo kryptis. Furjė spektrinio tankio vaizde matyti, kad energija sukaupta siaurame dažnių elipsiniame žiede. Žiedo matmenys priklauso nuo vidutinio periodo dydžio. Kuo periodas bus didesnis, tuo šviesus žiedas bus arčiau centro. Centro taškas atitinka nulinius dažnius x ir y kryptimi. Informacija apie kryptis atsispindi kompleksinio Furjė vaizdo fazėse, kurių reikšmės šiame paveikslėlyje nepavaizduotos, nes spektrinis tankis pagal apibrėžimą yra Furjė vaizdo modulis. Furjė vaizde fazės, kurios apibrėžiamos taip pat vienetinio ilgio krypties vektoriumi, elgiasi chaotiškai, todėl geriau vaizduoti orientacijas pradiniam vaizdui.

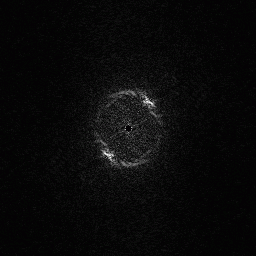
2-3 paveikslėlis. Piršto antspaudo ir jo Furjė spektrinio tankio vaizdai.

Orientacijos lauko taikymas pirštų antspaudams atpažinti

Susipažinkime detaliau kaip taikomas krypčių laukas pirštų antspaudų atpažinime. Pirštų antspaudams atpažinti taikoma klasikinė schema: pirminis apdorojimas, požymių išskyrimas, požymių sulyginimas su turimais duomenų bazėje ir sprendimų priėmimas apie piršto antspaudo priklausymą kokiam nors duomenų bazėje identifikuotam asmeniui. Pirštų antspaudų požymiai skirstomi į globalius ir lokalius. Globalūs požymiai yra trijų pagrindinių rūšių: sūkurio (spiralės) centro taškas, kilpos šerdies (angl. core) taškas ir delta taškas.

4 paveikslėlis. Trijų pagrindinių tipų globalieji pirštų antspaudų požymiai.

Žinant globaliuosius pirštų antspaudų požymius nesunku atmesti skirtingų tipų antspaudus, surasti poslinkio ir posūkio parametrus, norint lyginti tolimesnes pirštų antspaudų vaizdų detales. Sprendžiant globaliųjų požymių paieškos problemą pirma įvertinamas krypčių arba orientacijos laukas, o po to, taikant Puankarė indeksą, surandami globalieji požymiai.

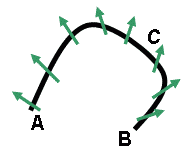Puankarė indeksas apibrėžiamas bet kokiam kontūrui patalpintam vektoriniame lauke. Yra skaičiuojamas bendras krypčių, kertančių kontūrą, kampų pokytis. Paveikslėlyje apskaičiuojant kontūro C Puankarė indeksą pradėsime nuo taško A, paimsime vektorinio lauko tame taške kryptį ir nuosekliai eisime link taško B skaičiuodami bendrą krypties pasikeitimą nuo pradinio taško A iki galinio B. Praktiškai informatyviausi yra uždarų kontūrų Puankarė indeksai. Žinoma bendra teorema apie galimas tokių kontūrų Puankarė indeksų reikšmes.

Jei kontūras C yra uždaras, kai galimos tik tokios Puankarė indekso reikšmės:

• 0 - kontūras riboja neypatingą taškus
• +360 - į kontūru ribojamą sritį patenka sūkurio taškas
• +180 - į kontūru ribojamą sritį patenka kilpos taškas
• -180 - į kontūru ribojamą sritį patenka delta taškas

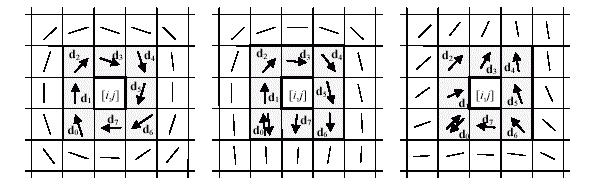
5 paveikslėlis. Punkarė indeksų galimos keturios skirtingos reikšmės.
Apačioje sūkurio (+360 laipsnių), kilpos (+180^o) ir delta (-180^o) atvejai.

Punkarė indekso ženklas priklauso nuo susitarimo kokia kryptimi (prieš ar pagal laikrodžio rodyklę) apeisite kontūrą. Tačiau pasirinkus vienodą apėjimo kryptį delta taško atveju visuomet gausite priešingo ženklo reikšmę lyginant su kilpos ir sūkurio atvejais.

Gali kilti klausimas kokią krytį pasirinki orientacijų atveju, nes žinant kokį kampą sudaro liestinė su x ašimis galima išvesti du priešingų krypčių vektorius, kurie abu bus lygiagretūs lygio linijos liestinei. Problema sprendžiama paprastai - fiksavus pradinio taško kryptį gretimuose taškuose kryptis parenkama taip, kad kampas moduliu trap gretimų vektorių būtų mažesnis.

Algoritmai

Vertinant orientacijas tenka vidurkinti gretimas orientacijos reikšmes. Ištirkime du atvejus, kai

1. dvi vidurkinamos gretimos reikšmės yra 0 ir 90 laipsnių;
2. 0 ir beveik 180 laipsnių.

Pirmu atveju turėtume gauti neapibrėžtą suvidurkintą kryptį, o antru - 0. Vidurkinimui įveskime svorius w, kurių reikšmės nuo 0 iki 1. Artimus nuliui svorius naudosime nepatikimai įvertintiems kampams sverti, o artimus 1 - patikimai įvertintiems kampams. Problemos gerai sprendžiasi, jei vidurkinamos netiesioginės kampų reikšmės y, bet jų kompleksiniai analogai:

e^2iy.

Šioje formulėje ypač svarbus daugiklis 2. Jo dėka kampai 2x0 ir 2x180 laipsnių pasidaro vienodi (kartotini pilnam apsisukimui). Taigi antru atveju, paėmę vienodus svorius w=0.5, gausime

0.5(e²ⁱ⁰ + e^2ip) = 1 eⁱ⁰,

o pirmu atveju

0.5(e²ⁱ⁰+e^2ip/2) = 0.

Gautą vidurkinto rezultato reikšmę patogu interpretuoti taip:

• gauto kompleksinio skaičiaus fazė nurodo kryptį;
• o modulis - patikimumą.

Kuo modulis arčiau 1, tuo rezultatas patikimesnis. Pirmuoju pavyzdžio atveju gavome 0 modulį. Vadinasi šiuo atveju kampas iš viso neapibrėžtas, kas dera su mūsų lūkesčiais.

Trumpai apibūdinsime pagrindines krypčių lauko / orientacijos įverčio algoritmų grupes.

Parametriniai metodai

Parametriniai metodai remiasi vaizdo funkcijos f(x,y) lokalia aproksimacija paprastomis išraiškomis. Radus aproksimaciją, orientacija įvertinama skaičiuojant aproksimacijos išraiškos gradientą ir imant jam statmeną kryptį, ne gradientas nukreiptas statmena lygio linijos liestinei kryptimi. Populiariausios yra tokios parametrinės aproksimacijos:

1. plokščiu paviršiumi: f(x,y) ~ ax + by + c;
2. paraboliniu paviršiumi: f(x,y) ~ ax² + by² + cxy + dx + ey + h.
3. cilindriniu paviršiumi: f(x,y) ~ a(x+ky)² + b(x+ky) + c.

Aproksimacijos parametrai randami paklaidos minimizavimu mažiausiųjų kvadratų metodu. Plokščio paviršiaus atveju gaunasi tokia formulė krypties kampų tangentui:

tg y = -E(xf(x,y))/E(yf(x,y)).

Čia E žymi lokalų vidurkinimą pasirinkto lango aplinkoje. Kitais dviem atvejais formulės žymiai sudėtingesnės.

Gradientiniai metodai

Gradientiniai metodai remiasi tuo faktu, kad funkcijos gradientas bet kuriame taške (x,y) yra statmenas lygio linijos liestinei tame pačiame taške. Idealiu tolydžiu atveju apskaičiuojame gradientą

( df/dx , df/dy )

ir jam statmena kryptis

( -df/dy , df/dx )

bus ieškoma liestinės orientacija, o tangentas orientacijos kampo bus apskaičiuojamas formule

tg y = -(df/dx)/(df/dy) .

Deja toks tiesmukiškas problemos sprendimas realiems vaizdams netinka, nes jų reikšmės visuomet žinomos su paklaidomis, dėl kurių tiesiogiai apskaičiuoti išvestines rizikinga. Išvestinių nestabilumo problema sprendžiama vidurkinant arba gretimų gradientų arba gautų orientacijų reikšmes. Pirmuoju atveju gauname formules

( df/dx , df/dy ) = 1 / ((2NX+1)(2NY+1)) S_{|n|≤NX, |m|≤NY} (df/dx_n,m , df/dy_n,m),

o antruoje atveju

( df/dx , df/dy ) = 1 / 2 arg S_{|n|≤NX, |m|≤NY} e^{-2iarctg(df/dx_n,m / df/dy_n,m)},

Gradientus galima įvertinti pagal tokias formules:

• (Kryžiaus tipo šablonas)
  (df/dx_n,m / df/dy_n,m) = 1/2(f(x+n+1,y+m)-f(x+n-1,y+m),f(x+n,y+m+1)-f(x+n,y+m-1))
• (2x2 tipo šablonas)
  (df/dx_n,m / df/dy_n,m) = 1/2(f(x+n+1,y+m+1)-f(x+n,y+m+1)+f(x+n+1,y+m)-f(x+n,y+m), f(x+n+1,y+m+1)-f(x+n+1,y+m)+f(x+n,y+m+1)-f(x+n,y+m))

Diferenciniai metodai

Diferenciniai metodai artimi gradientiniams metodams, tik šiuo atveju ieškoma kryptis, kuria skirtuminė išvestinė yra mažiausia. Pažymėkime funkcijos f gretimų reikšmių lentelę trumpai

f11	f12	f13
f21	f22	f23
f31	f32	f33

Tuomet išvestinės kryptimis 0, 45, 90 ir 135 laipsnių kampais galėsime aproksimuoti formulėmis

f'_0 = (f₁₃-f₁₁+f₂₃-f₂₁+f₃₃-f₃₁)/6;
f'_45 = (f₁₂-f₂₁+0.5(f₁₃-f₃₁)+f₂₃-f₃₂)/(3(2)^1/2);
f'_90 = (f₃₁-f₁₁+f₃₂-f₁₂+f₃₃-f₁₃)/6;
f'_135 = (f₂₃-f₁₂+0.5(f₃₃-f₁₁)+f₃₂-f₂₁)/(3(2)^1/2).

Apskaičiavus išvestinių reikšmes išsirenkama moduliu mažiausia ir laikoma, kad taške 22 orientacija yra mažiausią reikšmę atitinkantis kampas. Šiuo metodu nesunku įvertini ir krypties patikimumą:

w = (max_phi f'_phi - min_phi f'_phi) / max_phi f'_phi .

Projekciniai/dispersiniai metodai

Projekcinių metodų esmė tokia. Pasirenkama galima liestinės kryptis ir lygiagrečiai jai suvidurkinamos funkcijos f(x,y) reikšmės. Suvidurkintai vienmačiai funkcijai skaičiuojama dispersija. Liestinės kryptimi pasirenka ta kryptis, kurios atžvilgiu vidurkinant gaunama didžiausia vidurkintos funkcijos dispersija. Krypties patikimumo reikšmė skaičuojama panašia formule:

w = (max_psi D(psi) - min_psi D(psi)) / max_psi D(psi) .

Aprašytas vidurkinimas vadinamas Radono transformacija.

Spektriniai metodai

Spektriniai metodai labai paprasti. Pasirenkamas stačiakampis langas ir slenkamas vaizdu. Slenkančio lango centras apibrėžia tašką, kuriame vertinama orientacija. Tarkime šis taškas yra (x0,y0). Tuomet apskaičiuojama funkcijos

f_L(x,y) = f(x-x0,y-y0), |x-x0|≤L/2, |y-y0|≤L/2,

Furjė transformacija ir ieškomas jos modulio maksimumas išmetus mažą nulio aplinką. Tarkime Furjė modulio maksimali reikšmė buvo taške su indeksais (n0,m0). Tuomet orientacijos kampas tenkins lygtį

tg y(x0,y0) = -n0/m0.

Skirtingai nuo ankstesnių metodų, šiuo atveju negalima imti per daug mažo lango. Lango dydį apibrėžiančio parametro reikšmė turi būti tokia, kad į lango plotą patektų bent keletas vaizdo periodiškai beveik pasikartojančių elementų. Tačiau nesaikingas lango didinamas mažins tikslumą, nes bus integruojama informacija įvairias kryptis turinčio ploto. Taip pat lango didinimas lėtina algoritmo darbą.

Praktinis darbas

Realizuokite orientacijos įverčio algoritmą Java kalba.
Jūsų programa turi nuskaityti BMP arba GIF formato skaitmeninio vaizdo duomenis, apibrėžtus pilkumo lygmenimis. Jūsų algoritmas bus vertinamas pagal orientacijų lauko įverčio tikslumą testiniams duomenims ir rezultatų atsparumą duomenų paklaidoms.

Jūsų java klasė turi praplėsti šią abstrakčią java Orients klasę.

public static int nx=256, ny=256;
public static final double PI2 = 2*Math.PI;
public static double D = 8.0, alpha = -0.5;
public static int k = 1, noise = 0;