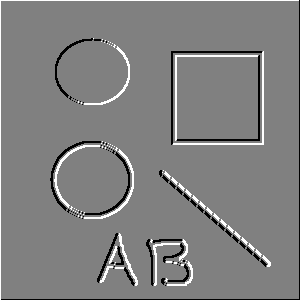
Lokalios orientacijos nustatymas

 
 
Piršto antspaudas   Orientacijos

Orientacijoms paskaičiuoti galima taikyti tokią formulę:

Gradientai (First Derivative)

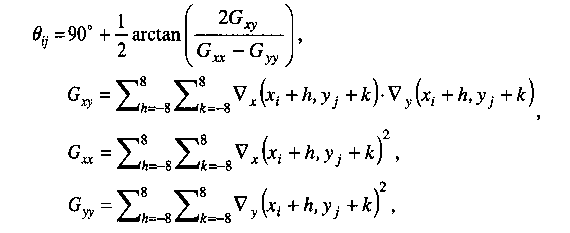Paprasčiausi horizontalaus gradiento operatoriai :[1. -1] (nesimetrinis: iš kiekvieno pradinio vaizdo pikselio atimamas (pradiniame vaizde) jo kaimynas iš dešinės ir rezultatas išsaugomas naujame vaizde pradinio pikselio vietoje) [-1 0. 1] (simetrinis: pikselio vietoje naujame vaizde įrašomas jo kaimynų skirtumas).
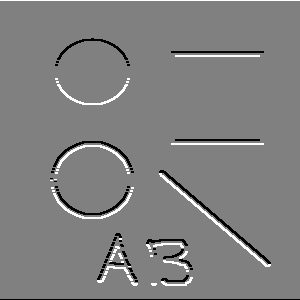
Gradientiniai operatoriai naudojami sričių kraštų paieškai.



-1 0 1
-1 0 1
-1 0 1
-1 -1 -1
0 0 0
1 1 1
-1 -1 1
-1 0 1
-1 1 1

Daugiau apie įvairius operatorius: http://www.mif.vu.lt/~pijus/SVA/vdkr.pdf


Orientacijų nustatymo žingsniai


Pradinis vaizdas:

 
 
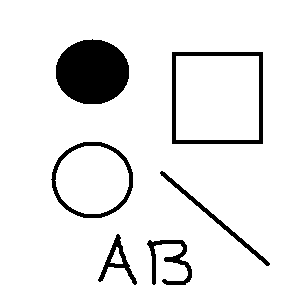
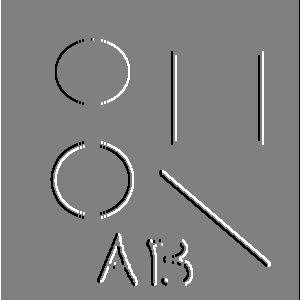
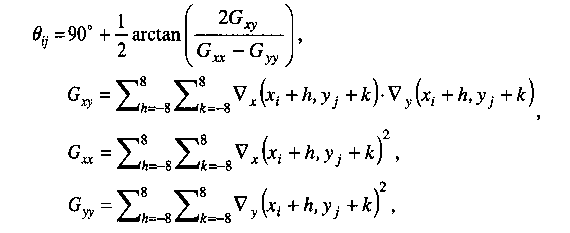Gx²       Gy²       Gx² * Gy²
 
           
 
 
Gxx       Gyy       Gxy
 
           



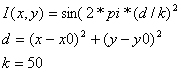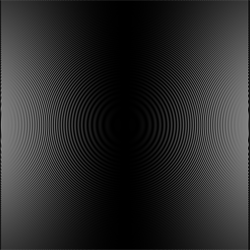
Pritaikius aukščiau aprašytą formulę, gauname:

     



Algoritmo įvertinimas - generuojame paveikslėlį:

                x, y - pikselio koordinatės
x0, y0 - apskritimų centras
d - atstumas nuo pikselio (x,y) iki centro
k - laisvai parenkama konstanta



Pvz:

                Paveikslėlio plotis - 501 pikselis
Paveikslėlio aukštis - 501 pikselis
x0 = 251
y0 = 251
k = 50



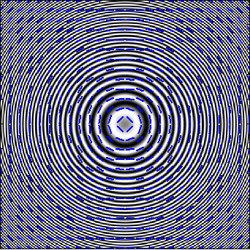
Šiame paveikslėlyje orientacija statmena apskritimų spinduliui, todėl mes galime ją įvertinti tiksliai.

Šiame pačiame paveikslėlyje apytiksliai randame orientaciją aukščiau aprašytu algoritmu (per gradientus).

Tiksliai paskaičiuotas orientacijas palyginame su paskaičiuotomis apytiksliai, t.y., kiekvienam pikseliui randame paklaidos kampą. Paklaidos kampas - nuo 0 iki 180 laipsnių.

Suvidurkinę paklaidas, gausime vidutinę algoritmo paklaidą šiam konkrečiam paveikslėliui. Paklaidą galima sumažinti parinkinėjant gradientų operatorių svorius bei kaitaliojant sumavimo lango dydį ir formą arba sumuojant su svoriniais koeficientais.

Kas yra sumavimas su svoriniais koeficientais?

Sumavimas be svorinių koeficientų: aplink kiekvieną pikselį uždedamas langas taip, kad pikselis būtų per vidurį ir lango ribose visų pikselių reikšmės susumuojamos. Rezultatas įrašomas pradinio pikselio vietoje naujame vaizde.
Sumavimas be svorių - tas pats, kaip sumavimas su svoriais, kai visi svoriai vienodi, pvz lygūs 1 arba vienetas, padalintas iš lango pikselių skaičiaus.
Kai langas kvadratinis, gali atsirasti paklaidos dėl to, kad lango kampuose esantys pikseliai, turintys tą patį svorį kaip kiti, iškreipia rezultatą. Todėl galima pamažinti svorius kampuose.

Pvz., vietoje

1 1 1
1 1 1
1 1 1


Galima naudoti

1 2 1
2 4 2
1 2 1