[Sinha, Poggio]

Veidų atpažinimas

  1. Išskirto veido dydžio normalizacija
  2. Veido pilkumo lygmenų normalizacija
  3. Požymių išskyrimas
  4. Požymių palyginimas
  5. Tikėtinumo santykio logaritmas
  6. Nuorodos
  7. Praktinis darbas
  8. Literatūra

Išskirto veido dydžio normalizacija

Veido segmentacija apytiksliai įvertina veido akių pozicijas. Laikysime, kad vaizde buvo išskirtas tik vienas veidas, kurio akių pozicijos nusakomos skaičiais

akys   =   {(xdešinės,ydešinės), (xkairės,ykairės)}   =   {(xd,yd), (xk,yk)}.

Koordinatės pateiktos įprastu būdu, t.y. koordinačių pradžios taškas yra viršutiniame kairiajame paveikslėio kampe. Šioje koordinačių sistemoje xdešinės < xkairės. Atliekant veido dydžio normalizaciją pasirenkamas standartinio dydžio stačiakampis ir jame nurodomos standartinės akių pozicijos. Paprastumo dėlei, kad būtų mažiau laisvų parametrų, naudosime tik akių koordinates standartinio dydžio vaizde, o stačiakampio dydį apibrėšime naudodami standartinių akių koordinates. Dėl simetrijos, natūralu laikyti, kad stačiakampio plotis yra dvigubai didesnis už akių vidurinio taško abscisę. Stačiakampio aukštį apibrėšime formule

H   =   (akių ordinatė) + 1.5 (atstumas tarp akių).

Gaunamo veido rezoliuciją lemia taškelių tarp akių skaičius. Fiksuokime konkrečias standartines akių koordinates:

akysstandartinės   =   { (100, 190), (230, 190) }.

Šiuo atveju atstumas tarp akių yra 130 vaizdo taškelių, o normalizuoto standartinio stačiakampio dydis:

((100 + 230)/2*2, 190 + 3*(230-100)/2   =   (330, 385 ).

Skaičiuojant taškeliais, prisideda po vienetą prie pločio ir ilgio ir gauname tokio dydžio standartinį stačiakampį:

Standartinis veido stačiakampis   =   331x386 taškelių vaizdas.

Kaip atvaizduoti pradinį vaizdą į šį stačiakampį? Postuluosime, kad atvaizdis yra standus, t.y. transformacija bet kokį trikampį atvaizduoja į trikampį išlaikydama pradinio trikampio kampus tarp kraštinių ir viršūnių orientaciją. Matematiškai standi transformacija aprašoma lygtimi

u   =   s cos(f) x - s sin(f) y + a,

v   =   s sin(f) x + s cos(f) y + b.

Čia (x,y) yra pradinio vaizdo taškelio koordinatės, o (u,v) standartinio dydžio stačiakampio koordinatės. Parametras s apibrėžia atvaizdžio mastelį; sąlyga s > 0 garantuoja, kad po atvaizdžio trikampio viršūnių orientacija nesikeičia. Parametras 0 ≤ f < 2 π apibrėžia posūkio kampą tarp pradinės x ašies ir pasuktos u ašies; kampo reikšmė matuojama radianais prieš laikrodžio rodyklę. Parametrų a ir b pora nusako poslinkį. Taškas (a,b) yra (x,y) koordinačių pradžios taško koordinatės naujoje (u,v) koordinačių sistemoje.

Turint akių koordinates pradinėje ir naujojoje koordinačių sistemoje, t.y.

{(xdešinės,ydešinės), (xkairės,ykairės)}   =   {(xd,yd),(xk,yk)}

ir

{(udešinės,vdešinės), (ukairės,vkairės)}   =   {(ud,vd),(uk,vk)}   =   {(100,190),(230,190)}

lengvai rasime standžios transformacijos parametrus:

s cos(f) = ((xd-xk)*(ud-uk)+ (yd-yk)*(vd-vk))/ ((xd-xk)2+(yd-yk)2),

s sin(f) = ((xd-xk)*(vd-vk) - (yd-yk)*(ud-uk))/ ((xd-xk)2+(yd-yk)2),

a   =   uk - s cos(f) xk + s sin(f) yk,

b   =   vk - s sin(f) xk - s cos(f) yk.

Naudojantis šiomis formulėmis nesunku apskaičiuoti mastelio s ir posūkio kampo f reikšmes, tačiau standžios transformacijos formulei apibrėžti pakanka žinoti s cos(f) ir s sin(f) reikšmes, kurias apskaičiavome nenaudodami nei šaknies traukimo, nei arktangento operacijų; tai spartina skaičiavimus.

Atvirkštinė transformacija, t.y. originalios (x,y) koordinatės, apskaičiuojamos žinant naujas (u,v) koordinates pagal formules

x   =   s-1 cos(f) u + s-1 sin(f) v + a',

y   =  -s-1 sin(f) u + s-1 cos(f) v + b',

a'   =   -s-1 cos(f) a - s-1 sin(f) b,

b'   =  s-1 sin(f) a - s-1 cos(f) b.

1 paveikslėlis. Originali nesegmentuoto veido nuotrauka,
MBGC target original 02463d634.jpg, 2272x1704 taškelių,
akių pozicijos: {(1138,227), (1291,230)}.
Nuotraukoje yra MBGC veido duomenų bazės koordinatoriaus Kevin W. Bowyer veidas.

2 paveikslėlis. Normalizuotas standartinio dydžio segmentuotas veidas, 331x386 taškelių, akių pozicijos: {(100,190), (230,190)}.

Žinant atvirkštinės transformacijos formules, normalizuoto dydžio vaizdas RGB(u,v) gaunamas pagal formulę

RGB(u,v) = rgb( s-1 cos(f) u + s-1 sin(f) v + a', -s-1 sin(f) u + s-1 cos(f) v + b' ),

kur rgb(x,y) yra pradinio originalaus vaizdo R,G ir B spalvų komponentės. Skaičiuojant pagal parašytas formules gaunamos nesveikaskaitės koordinatės (x,y). Todėl atliekant praktinius skaičiavimus rgb(x,y) reikšmė dažniausiai pakeičiama bitiesine interpoliacija panaudojant sveikaskaičių koordinačių rgb[i,j], rgb[i+1,j], rgb[i,j+1] ir rgb[i+1,j+1] reikšmes, kur i = [x] ir j = [y] yra x ir y sveikosios dalys.

1 pav. pateikia originalios veido nuotraukos vaizdą. Ši nuotrauka paimta iš MBGC target original kolekcijos; nuotraukoje yra MBGC duomenų rinkinio koordinatoriaus Kevin W. Bowyer veidas.
2 pav. pateiktas segmentuotas iki standartinio dydžio 331x386 veidas. Segmentacijai naudotos tokios akių pozicijos: {(1138,227), (1291,230)}.

Programos derinimui galite pasinaudoti konkrečiomis lygtimis, kurios gaunasi pateiktų paveikslėlių duomenims:

  u   =   0.8493466564181399 x  +  0.01665385600819882 y  -  870.3369203177044
  v   =   -0.01665385600819882 x  +  0.8493466564181399 y  +  16.1503971304125
  x   =   1.176923076923077 u  -  0.023076923076923078 v  +  1024.6923076923078
  y   =   0.023076923076923078 u  +  1.176923076923077 v  +  1.0769230769230802

Taip pat naudinga patikrinti, kad įstačius į pirmas dvi jūsų gautas lygtis x = xk, y = yk, turite gauti u = uk, v = vk. Analogiškai, įstačius į trečią ir ketvirtą lygtį reikšmes u = ud, v = vd, turite gauti x = xd, y = yd. Kadangi mūsų atveju gavome mažą kampo f = -0.02 vertę, tai reiškia, kad segmentuojamo veido akis jungianti tiesė sudaro mažą kampą su horizonto linija. s = 0.85 vertė artima vienetui. Tai rodo, kad normalizuoto iki standartinių akių pozicijų paveiksllėlio rezoliucija mažai pasikeitė. Konkrečiau, 1-as originalaus vaizdo taškelis atitinka 0.85 segmentuoto veido taškelių (s = 0.85) ir 1-as segmentuoto paveikslėlio taškelis atitinka 1.18 originalaus paveikslėlio taškelių (s-1 = 1.18). Taigi mūsų atveju segmentacijos mastelis yra 1 : 1.18.

Dar viena naudinga informacija yra nejudamas transformacijos taškas. Pagal nejudamo taško apibrėžimą originalaus vaizdo plokštumos taškas (x,y) (nebūtinai sveikaskaičių reikšmių ir nebūtinai priklausantis originaliam vaizdui ) vadinamas nejudamu, jei to paties taško koordinačių reikšmės gautos segmentuotą vaizdą atitinkančioje plokštumoje, lieka nepakitusios. Kitaip tariant nejudamas taškas tenkina lygtis x = u ir y = v . Galimi trys kokybiškai skirtingų segmentacijų atvejai.

  1. Segmentuotas ir originalus vaizdas neturi nejudamo taško.
    Taip bus tada ir tik tada, kai segmentacijos mastelis yra 1:1, segmentacijos posūkio kampo f reikšmė yra kartotinė 2 π ir segmentuotas ir originalus vaizdai nesutampa. Kitaip tariant šiuo atveju vaizdai yra paslinkti vienas kito atžvilgiu.
  2. Visi segmentuoto ir originalaus vaizdo taškai yra nejudami.
    Taip bus tada ir tik tada, kai segmentacijos mastelis yra 1:1, segmentacijos posūkio kampo f reikšmė yra kartotinė 2 π ir segmentuotas ir originalus vaizdas sutampa. Paprastai kalbant abu vaizdai šiuo atveju sutampa.
  3. Segmentuotas ir originalus vaizdas turi tik vieną nejudamą tašką.
    Taip bus tada ir tik tada, kai segmentacijos mastelis yra ne 1:1 arba posūkio kampo reikšmė yra nekartotinė 2 π ( pakanka bent vienos sąlygos ).

Kadangi mūsų segmentacijos pavyzdžio s ≠ 1 ( ir f ≠ 0 ), segmentaciją atitinkanti transformacija turės tik vieną nejudamą tašką. Nejudamo taško koordinatės yra

x = u = -5695.631970260222,
y = v = 736.82156133829.

Nejudamo taško koordinates taip pat galite panaudoti programos derinimui. Paprasčiausiai įstatykite šias koordinates į (x,y) ir (u,v) sąryšių lygtis ir turite gauti nepakitusias koordinates.

Veido pilkumo lygmenų normalizacija

Literatūroje yra daug informacijos apie veido spalvos panaudojimą jo segmentacijai. Tačiau lyginant segmentuotus veidus dažniausiai atsisakoma spalvinės informacijos ir lyginamos veidų tekstūros pateiktos pilkumo lygmenimis. Pastebėta, kad baltaodžių ir geltonodžių veiduose dominuoja raudonoji ir žalioji komponentės, o mėlynojoje santykinai būna daug triukšmo. Todėl perėjimo prie pilkumo lygmenų formulėje

grey   =   a r + b g + c b

rekomenduojame paimti svorius a=0.5, b=0.5 ir c=0. Skrupulingai optimizuojant veidų atpažinimo kokybę galima parinkti ir kitus svorius, tačiau mes fiksuosime šį paprastą variantą.

3 paveikslėlis. Segmentuoto veido pilkumo lygmenys, naudota formulė grey = ( r + g ) / 2.

3 pav. iliustruoja segmentuotą MBGC 02463d634 veidą pateiktą pilkumo lygmenimis. Praktiškai pastebėta, kad tiesiogiai skaičiuojant veidų požymius naudojantis veido pilkumo lygmenų vaizdu gaunasi nestabilūs požymiai. Pagrindinis požymių nestabilumo šaltinis yra veido apšvietimas. Kintant apšvietimo šaltinio spektrui ir pozicijai gaunasi skirtingų pilkumo lygmenų vaizdai, o tai kenkia atpažinimo kokybei. Kad kiek eliminuoti apšvietimą, atliekama taip vadinama veido normalizacija. Normalizacijos pagrindinė idėja išnaudoti apšvietimo stiprio santykinai lėtą kitimą gretimuose taškeliuose. Praktiškai normalizacija atliekama dažnai tokiu būdu:

  1. Atliekamas pilkumo lygmenų vaizdo vidurkinimas σ1 masteliu;
  2. Atliekamas pilkumo lygmenų vaizdo vidurkinimas σ2 > σ1 masteliu;
  3. Normalizuotas vaizdas apibrėžiamas dviejų vidurkintų vaizdų santykiu arba skirtumu.

Kad realizuoti šią procedūrą, reikia pasirinkti vaizdo vidurkinimo būdą. Teoriškai tam tikra prasme optimalus vidurkinimas naudoja Gauso filtrą. Gauso funkcijos vidutinio kvadratinio nuokrypio dydis σ apibrėžia vidurkinimo mastelį. Gauso vidurkinimas yra invariantiškas vaizdo posūkiui, tačiau vidurkinimo procedūra yra lėta. Vidurkinimas sparčiai atliekamas vidurkinant pasirinkto dydžio kvadrato formos slenkamuoju vidurkinimo langu, t.y. vidurkinimo filtras yra lygus 1, kai indeksai patenka į 2σ dydžio kvadratą, kurio vidurys yra taške (0,0), kitais atvejais filtro reikšmė yra nulis. Tačiau vidurkinimo rezultatas panaudojant šį filtrą gana jautrus vaizdo posūkiui ir poslinkiui, nes filtras yra trūkus, t.y. jo reikšmės šuoliu pereina nuo 0 iki 1 ir atvirkščiai. Todėl mes ieškosime tarpinio filtro, kuris būtų tolydus ir kuris leistų sparčiai atlikti skaičiavimus.

Aprašydami mūsų siūlomą vidurkinimo filtrą plokštumos taško koordinates žymėsime (x,y), pilkumo lygmenis u(x,y), o filtrą f(x,y). Pradžioje aprašysime filtrą vienmačiu atveju, t.y. kai u=u(x) ir f = f(x), o dvimatis filtras išsiskaidys į filtravimą x ir y kryptimis paeiliui.

Gerai žinoma idėja greitai apskaičiuoti signalo vidurkį duotame stačiakampyje lange. Jei turima apskaičiuota vidurkinimui reikalinga suma

u_[i]   =   Σ |j-i|< 1/σ u[j],

tai sekanti suma apskaičiuojama efektyviai panaudojant prieš tai apskaičiuotos sumos reikšmę:

u_[i+1]   =   Σ |j-i-1|< 1/σ u[j]   =   u[i]_ - u[i-1/σ] + u[i+1/σ].

Toks vidurkinimo būdas vadinamas vidurkinimu panaudojant slenkantį langą. Tačiau slenkančio lango filtras yra trūkus, o tai silpnina vidurkinimo kokybę. Todėl mes remsimės simetriniu eksponentiniu filtru, kuris tolydžiu atveju apibrėžiamas išraiška

fσ(x)   =   exp(-|x|/σ)/(2&sigma).

Filtro apibrėžime naudojamas 1/(2σ) daugiklis, kad filtro atsakas į konstantą būtų ta pati konstanta. Šio filtro nenormuotas diskretus analogas yra

fσ[i]   =   exp(-|i|/σ).

Filtravimą šiuo filtru patogu išskaidyti į dvi dalis:

(u*f)[i] = Σ_j ≥ 0 u[i-j] exp(-j/σ) + Σ_j < 0 u[j-i] exp(j/σ).

Pirmoji filtravimo suma naudoja signalo reikšmes u[n], n ≤ i, todėl šis filtras yra fiziškai realizuojamas; antroji suma naudoja signalo reikšmes u[n], n > i. Laikysime, kad žinomos signalo reikšmės u[n], 0 ≤ n < N ir jas pratęsime tolydžiai konstantomis: u[n] = u[0], kai n < ir u[n] = u[N-1], kai n ≥ N-1. Panašiai kaip ir slenkančio vidurkio atveju, jei žinoma pavyzdžiui

(u*f+)[i] = Σ_j ≥ 0 u[i-j] exp(-j/σ)

filtravimo reikšmė, tai sekanti reikšmė greitai apskaičiuojama formule

(u*f+)[i+1] = Σ_j ≥ 0 u[i+1-j] exp(-j/σ) = exp(-1/σ) (u*f+)[i] + u[i+1].

Saugojant

q   =   exp(-1/σ)

atskira konstanta, gauname tas pačias skaičiavimo sąnaudas kaip ir slenkančiame vidurkyje. Pagal mūsų prielaidą u[n] = u[0] visiems n < 0. Todėl rekursinius skaičiavimus į priekį galime pradėti nuo reikšmės

(u*f+)[0] = Σ_j ≥ 0 u[-j] exp(-j/σ) = u[0] / ( 1 - exp(-1/σ)).

Analogiškai antrajai filtravimo sumai gauname

(u*f-)[i] = Σ_j < 0 u[i-j] exp(j/σ),

(u*f-)[i-1] = exp(-1/σ) ((u*f-)[i] + u[i-1]).

Čia mes sąmoningai parašėme rekurentinę išraišką (u*f-)[i-1] nariui, o ne (u*f-)[i+1]. Rekurentinį ryšį galima parašyti ir pastarajam nariui, tačiau rekursijoje būtų dėmuo exp(1/σ) ((u*f-)[i], kuris pasižymėtų nestabilumu, nes exp(1/σ) > 1 (laikoma, kad σ > 0). (u*f-)[i] skaičiuojama nuo galo, t.y. pradžioje apskaičiuojamas

(u*f-)[N-1] = Σ_j < 0 u[N-1-j] exp(j/σ) = u[N-1] exp(-1/σ) / ( 1 - exp(-1/σ)),

o toliau nariams (u*f-)[N-2], (u*f-)[N-3], ..., (u*f-)[0], apskaičiuoti naudojama viršuje parašyta rekursija.

Atsakas diskretaus simetrinio eksponentinio filtro į konstantą yra

(1*f)[i] ≡ ( 1 + exp(-1/σ)) / ( 1 - exp(-1/σ)),

todėl apibrėžiant pradinį simetrinį eksponentinį filtrą, galima jį padalinti iš šios konstantos. Vienas slenkančio vidurkio žingsnis reikalauja vienos sudėties ir vienos atimties veiksmo. Simetrinio eksponentinio filtro atveju gauname dvi daugybas ir du atimties veiksmus, kas tik dvigubai sudėtingiau už slenkančio vidurkio filtravimą.

Kad būtų lengviau derimti programas, pateiksime trumpo vienmačio filtravimo pavyzdį.

σ = 1/log(4./3) = 3.4761, q = exp(-1/σ) = 3/4,
N = 4, u[0] = 256, u[1] = 64, u[2] = 128, u[3] = 32,

(u*f+)[0] = Σ_j ≤ 0 u[j] exp(j/σ) = u[0] / ( 1 - exp(-1/σ)) = 256 / ( 1 - 3/4 ) = 1024,
(u*f+)[1] = 832, (u*f+)[2] = 752, (u*f+)[3] = 596,

(u*f-)[N-1] = Σ_j > N-1 u[j] exp( (j-N)/σ) = u[N-1] exp(-1/σ) / ( 1 - exp(-1/σ)) = 32 * 3/4 / ( 1 - 3/4 ) = 96,
(u*f-)[2] = 96, (u*f-)[1] = 168, (u*f-)[0] = 174.

Galutinės normuotos iš daugiklio

( 1 - exp(-1/σ)) / ( 1 + exp(-1/σ)) = ( 1 - 3/4 ) / ( 1 + 3/4 ) = 0.142857

filtravimo reikšmės (u*f)[n] = (u*f+)[n] + (u*f-)[n] yra

(u*f)[0] = 171.142857, (u*f)[1] = 142.857143, (u*f)[2] = 121.142857, (u*f)[3] = 98.857143.

Dvimatis filtravimas simetriniu eksponentiniu filtru

fσ1,σ2 = exp(-|x|/σ1)exp(-|y|/σ2)

atliekamas paeiliui filtruojant vaizdo eilutes su filtru fσ1 = exp(-|x|/σ1) ir gauto filtruoto vaizdo stulpelius filtruojant su simetriniu eksponentiniu filtru fσ2 = exp(-|y|/σ1), bei, jei norima, padauginant iš normavimo konstantos, kad konstantinio vaizdo filtravimo rezultatas išliktų ta pati konstanta.

5 paveikslėlis. Veido filtravimo normuotu f1,1 dvimačiu simetriniu filtru rezultatas.

5 pav. pateiktas filtravimo dvimačiu eksponentiniu filtru rezultatas, kurio parametrai yra σ1 = σ2 = 1. Gautas vidurkinimo eksponentiniu filtru rezultatas mažai skiriasi nuo pradinio pilkumo lygmenų vaizdo. Taip yra dėl dviejų priežasčių. Ribiniu atveju, kai σ artėja į +0, eksponetinis simetrinis filtras artėja į vienetinį operatorių. Kadangi vienetinis operatorius pradinio vaizdo nekeičia, tai filtruojant su mažomis σ vertėmis gauname artimą pradiniam vaizdui rezultatą. Kita priežastis yra simetrinio filtro "aštrumas" nulio taške x. Dėl šios priežasties simetrinis eksponentinis filtras neturi išvestinės taške x = 0, o tai filtro nepuošia. Kad ištaisyti šią simetrinio eksponentinio filtro ydą, komponuosime fσ1,σ1, fσ1,σ2, fσ2,σ1 ir fσ2,σ2 filtrus.

(σ1 exp(-|x|/σ1) - σ2 exp(-|x|/σ2) )

ir

(σ1 exp(-|y|/σ1) - σ2 exp(-|y|/σ2) )

yra tolydžiai diferencijuojami filtrai. Todėl jų sandauga

(σ1 exp(-|x|/σ1) - σ2 exp(-|x|/σ2) ) (σ1 exp(-|y|/σ1) - σ2 exp(-|y|/σ2) )   =  

(σ1 σ1 fσ1,σ1 - σ1 σ2 ( fσ1,σ2 + fσ2,σ1 ) + σ2 σ2 fσ2,σ2

taip pat tolydžiai diferencijuojama. Iš pateiktos išraiškos matyti, kad naujas tolydžiai diferencijuojamas filtras yra keturių simetrinių eksponentinių dvimačių filtrų tiesinis darinys. Bendras sukonstruoto vidurkinimo filtro sudėtingumas yra

4*2 + 3 = 11 daugybos ir 4*2 + 3 = 11 sudėties/atimties

veiksmų taškeliui.

5 paveikslėlis. Veidas vidurkintas tolydžiai diferencijuojamu eksponentinio tipo filtru su parametrais σ1 = 1 ir σ2=3.

5 paveikslėlis iliustruoja veidą vidurkintą tolydžiai diferencijuojamu filtru. Vidurkinimo filtras buvo apibrėžtas išraiška

( f1,1 - 3 (f1,3 + f3,1 ) + 9 f3,3.

Gautas vidurkintas vaizdas labiau skiriasi nuo pradinio ir yra žymiai glodesnis. Jei pradiniame vaizde būtų kokioje nors dalyje didelis atsitiktinis triukšmas, tai toks vidurkinimas efektyviai sumažintų triukšmo amplitudę. Filtro savybes gerai atspindi jo atsakas į vienetinį delta signalą. Dvimačiu atveju toks etaloninis signalas yra juodame stačiakampio viduryje patalpintas vienas baltas taškelis. Atlikus tokiam vaizdui filtravimą gaunasi vaizdas, kuriame matyti filtro koeficientai.

a)   b)   c)  

6 paveikslėlis. a) Filtruojamas etaloninis vienetinis "delta" vaizdas (kairėje)
b) Eksponentinio dvimačio filtro f1,1 atsakas į delta signalą (viduryje)
c) Tolydžiai diferencijuojamo eksponentinio filtro ( f1,1 - 3 (f1,3 + f3,1 ) + 9 f3,3 ) atsakas į delta signalą (dešinėje)

Iš pateiktų 6 pav. iliustracijų matyti, kad tolydžiai diferencijuojamo filtro koeficientai yra labiau invariantiški posūkio atžvilgiu ir jie labiau išplitę plokštumoje. Tai ir lemia didesnį vaizdo glodumą, kai yra filtruojama šiuo filtru.

Dabar esame pasirengę atlikti veido normalizaciją. Tuo tikslu mums reikia gauti du skirtingais masteliai vidurkintus vaizdus ir imant gautų vaizdų santykį arba skirtumą gauti normalizuotą vaizdą. Vidurkinimui naudosime du tolydžiai diferencijuojamus dvimačius eksponentinius filtrus

( σ1 σ1 fσ1,σ1 - σ1 σ2 ( fσ1,σ2 + fσ2,σ1 ) + σ2 σ2 fσ2,σ2 )

Pirmu atveju fiksuosime

σ1 = 2-1/8, σ2 = 21/8,

antru

σ1 = 2-1/83, σ2 = 21/83

a) b)

7 paveikslėlis. Vidurkintas veidas su glodžiais filtrais:
a) σ1 = 2-1/8, σ2 = 21/8
b) σ1 = 2-1/83, σ2 = 21/83

7 pav. iliustruoja gautus vidurkinimo rezultatus. Normalizuotą vaizdą apibrėšime išraiška

norm(x,y) = 128 + const del(x,y),

del(x,y) = ( u1(x,y) - u2(x,y) ) / ( ( u1(x,y) + u2(x,y) ) / 2).

Čia u1 ir u2 vidurkinti 7 pav. a) ir b) veidai. Adityvi konstanta 128 paslenka vaizdą iki vidutinio pilkumo lygmens, o daugiklio const reikšmė parenkama taip, kad gauto normalizuoto veido pilkumo lygmenys kistų nuo 0 iki 255. Jei vaizdas (x,y) aplinkoje mažai keičiasi, tai del(x,y) reikšmė bus maža ir normalizuoto vaizdo reikšmė bus arti 128. Kad išryškinti mažas reikšmes, normalizacijai galima naudoti papildomą dėmenį sgn(del(x,y)) sqrt(|del(x,y)|) = del(x,y) / sqrt(|del(x,y)|). Žemiau pateiktoje iliustracijoje 8 pav. b) panaudota tokia išraiška:

norm(x,y) = 128 + const ( del(x,y) + 0.25 del(x,y) / sqrt( |del(x,y)| ) ).

a) b)

8 paveikslėlis. Normalizuotų pilkumo lygmenų veidai.
a) Normalizacija atlikta panaudojant norm(x,y) = 128 + const del(x,y) formulę.
b) Normalizacija atlikta panaudojant norm(x,y) = 128 + const ( del(x,y) + 0.25 del(x,y) / sqrt( |del(x,y)| ) ) formulę.

Kaip ir reikėjo tikėtis, 8 pav. b) normalizacija labiau išryškina smulkius tekstūros pokyčius, lyginant su 8 pav. a) normalizacija. Abi normalizacijos ženkliai sumažina dėl apšvietimo kilusius veido pilkumo lygmenų pokyčius. Nesunku pastebėti kaip sumažėjo šešėlių įtaka vaizdui, tačiau ji pilnai nėra eliminuota ir vargu ar galima tikėtis idealaus veido normalizavimo algoritmo. Kuris normalizacijos variantas pranašesnis vizualiai sunku spręsti, tai išryškėja vėlesniuose etapuose kai atpažįstami veidai ir įvertinama veidų atpažinimo kokybė.

Požymių išskyrimas

Dažniausiai naudojami požymiai veidams atpažinti

Veidų atpažinimo algoritmus galima suskirstyti į dvi stambias kategorijas: globalių (holistic) ir lokalių (local) požymių lyginimo algoritmus. 1987 metais pasirodė „tikrinio veido“ (angl. eigenface) - pirmasis metodas veidų atpažinimui (L. Sirovich and M. Kirby "Low-dimensional procedure for the characterization of human faces”, Journal of the Optical Society of America, p. 519-524). Tikrinių veidų metodas yra pagrindinių komponenčių metodo (angl. Principal Component Analysis – PCA) dalinis atvejis. Šio metodo viena pirmųjų realizacijų (1991 m, Matthew Turk and Alex Pentland, “Eigenfaces for recognicion”, Journal of Cognitive Neuroscience, p. 71-86) atskleidė metodikos trūkumus ir dėl prastų veido atpažinimo rezultatų yra naudojama dažniausiai kaip apatinis atramos taškas kitų algoritmų rezultatams palyginti. PCA metodo modifikacijos naudoja dažnai atskirų veido komponenčių tikrines reikšmes ir bazines funkcijas, tačiau tuo pačiu tolstama nuo holistinės veido reprezentacijos ir tai byloja apie principines holistinio metodo ydas.

Lokalūs binariniai vaizdai

LBP (angl. Local Binary Patterns) metodas buvo sukurtas tekstūroms aprašyti ir palyginti 2004 metais LBP metodas buvo pritaikytas atpažinti veidams (T. Ahonen, A. Hadid, M. Pietikainen, „Face Description with Local Binary Patterns: Application to Face Recognition“, p. 1-15). Dėl savo paprastumo ir santykinai neblogų rezultatų LBM metodas labai išpopuliarėjo. Metodo esmė (Tado Kazakevičiaus bakalauro darbo iliustracija ) yra tokia: veidas pirma padalinamas į mažus lokalius regionus (angl. local blocks, iš kurių gaunamos LBP histogramos, kurios yra sujungiamos į vieną (2 pav.). Atpažinimas yra atliekamas lyginant histogramų artumą. Matematinės statistikos terminais histogramos atspindi taškelių skirstinį, todėl lyginant histogramas galima naudotis matematinės statistikos metodais.

LBP histogramos jautriai reaguoja į įvairius šviesos pasikeitimus, kartu ir į triukšmą. Charakteringos veido paveikslėlio zonos, kuriose yra santykinai daug triukšmo, yra kakta ir skruostai. Sekanti požymių grupė yra bene populiariausia ir yra gana atspari aprašytam triukšmui.

Gaboro lokalūs požymiai ir Gaboro tūtos

Gaboro požymiai gaunami filtruojant veidą įvairių parametrų Gaboro filtrais. Gaboro filtrus Daugmanas (http://www.cl.cam.ac.uk/~jgd1000/) sėkmingai pritaikė išskiriant akies rainelės binarinius požymius. Gabor filtrus taiko praktiškai visos veidų atpažinimo sistemos; vieni pirmųjų darbų paskelbti Jie Zou, Qiang Ji, George Nagy, „A Comparative Study of Local Matching“. IEEE Transactions on image processing. Volume 16, NO 10, p.2617-2628, Shiguang Shan, Peng Yang, Xilin Chen, and Wen Gao. AdaBoost Gabor Fisher Classifier for Face Recognition, p. 278-290, Wiskott, L.; Fellous, J.-M.; Kuiger, N.; von der Malsburg, C. „Face recognition by elastic bunch graph matching“. Pattern Analysis and Machine Intelligence, IEEE Transactions on image processing. Volume 19, Issue 7, Jul 1997, p. 775 – 779 straipsniuose.

Gaboro filtrai yra Gauso (Gaussian) ir sinuso bei kosinuso funkcijų sandaugos. Kadangi filtrai taikomi vaizdams, tai visos funkcijos yra dviejų kintamųjų x ir y. Gauso funkcijos reikšmės priklauso tik nuo taško (x,y) atstumo iki koordinačių pradžios ir turi vieną laisvą parametrą sigmą, kuris apibrėžia funkcijos mastelį. Sinusas ir kosinusas dažniausiai apjungiami į vieną kompleksinę eksponentę ir turi du laisvus parametrus: krypties vektorių ir dažnį. Matematiškai Gaboro filtras apibrėžiamas tokia išraiška:
Gabor filtras:

G(x,y) = s(x,y) wσ(x,y),

kur s(x, y) yra kompleksinė eksponentė, wσ(x,y). Gauso(Gaussian) formos gaubiančioji funkcija (angl. envelope) (3 pav.).

Gauso funkciją galima užrašyti:

s(x,y) = exp( -(x2+y2) /(2 σ2) ),

kur σ atspindi Gauso funkcijos mastelį. Mažiems sigma Gauso funkcijos grafikas „siauras“, dideliems – išplitęs. Kompleksinę eksponentę galima išskaidyti į realią ir menamą dalis:


kur θ fazė(angl. phase), α - filtro kryptis (angl. angle), f – kompleksinės eksponentės dažnis (angl. frequency).

Tarkime, kad I(x, y) yra paveikslėlio pilkumo lygmenų intensyvumo funkcija, o G(x,y) Gabor filtras. Tai Gabor reprezentaciją R(x, y) galima aprašyti:

R(x, y)=I(x, y)*G(x,y),

kur * - sąsūkos operacija.

Daugumoje veidų atpažinimo sistemų, naudojančių Gabor filtrus, naudojami aštuonių orientacijų ir penkių mastelių Gabor filtrai (6 pav., Tado Kazakevičiaus iliustracija).

Taigi veido regiono taškuose atliekamos sąsūkos operacijos ir kiekviename taške gaunama bruožų tūta (Gabor jet), kuri charakterizuoja regioną, esantį apie tą tašką. Šių bruožų tūtų visuma apibūdina veido esminius požymius. Veidų panašumas skaičiuojamas lyginant kiekvieno veido gautas tūtas. Yra žinoma ir vykdant testavimus, buvo pastebėta, kad Gabor metodas yra atsparus apšvietimo kitimui ir mažam veido nuokrypiui po išlyginimo etapo. Tačiau papildomai atlikta veido pilkumo lygmenų normalizacija dar labiau pagerina atpažinimo kokybę.

Šiuo metu veidų atpažinime vyrauja Gaboro požymiai. Gaboro požymiai naudoja įvairaus mastelio Gauso funkciją padaugintą iš kompleksinių eksponenčių. Fiksavus Gauso funkcijos centrą yra skaičiuojami vaizdo atsakai į kelių mastelių (6-12) ir kelių krypčių (6-16) filtrus. Visas atsakų rinkinys fiksuotam centrui vadinamas Gaboro požymių tūta (Gabor jet). Gaboro požymių privalumas, kad imant kosinuso ir sinuso komponenčių kvadratų sumą gauname atsparius mažiems poslinkiams požymius. Pagrindinis jų trūkumas - jie lėtai apskaičiuojami ir todėl dažnai Gaboro požymiai įvertinami tik išretintame centrų tinklelyje, o tai menkina jų gebėjimą atskirti skirtingus veidus.

Teiloro binariniai požymiai

Apskaičiuodami veido požymius remsimės normalizuotais veido vaizdais. Lyginant vidurkintas tekstūras stengsimės įvertinti pilkumo lygmenų kitimo tendenciją pasirinkto taško aplinkoje. Vaizdo pilkumo lygmenis galime įsivaizduoti dviejų kintamųjų funkcija u=u(x,y). Iš matematinės analizės gerai žinoma, kad glodžią funkciją galima gerai aproksimuoti taško aplinkoje žinant funkcijos išvestines tame taške. Nors vaizdai yra suvidurkinti, tačiau skaičiuojant aukštesnės eilės išvestines gaunamos nestabilios stipriai osciliuojančios reikšmės. Todėl naudosime tik pirmos ir antros eilės išvestines:

ux(x,y) = u(x+h,y) - u(x-h,y), uy(x,y) = u(x,y+h) - u(x,y-h),
uxx(x,y) = u(x+h,y) - 2u(x,y) + u(x-h,y), uyy(x,y) = u(x,y+h) - 2u(x,y) + u(x,y-h),

Psichofiziologai išsiaiškino, kad žmogaus regos sistema remiasi skirtingomis kryptimis ir skirtingais masteliais filtruotais vaizdais. Imituodami šias regos ypatybes, pasirinksime keturias kryptis

α = 0, π/4, π/2, 3π/4,

ir keliais skirtingais masteliais σ vidurkinsime veido vaizdus. Fiksuotai krypčiai gauname tokias išvestines:

u′(x,y;α) = u(x+h cos(α),y+h sin(α)) - u(x-h cos(α),y - h sin(α)),
u′′(x,y;α) = u(x+h cos(α),y+h sin(α)) - 2u(x,y) + u(x-h cos(α),y-h sin(α)).

Šiose formulėse trukmeninės h cos(α) ir h sin(α) reikšmės apvalinamos iki artimiausiojo sveikojo skaičiaus. Kad taupyti požymiams saugoti reikalingus resursus ir vėliau būtų galima sparčiai atlikti dviejų veidų požymių palyginimą, saugosime tik išvestinių ženklus. Toks požymių pasirinkimas maksimaliai stabilizuoja požymio reikšmę. Tarkime, vaizdo išvestinės ženklo pasikeitimas dėl triukšmo reiškia, kad vaizdas taško aplinkoje pakeitė savo didėjimo arba mažėjimo kryptį. Kadangi mūsų vaizdai yra intensyviai vidurkinami, tai toks pasikeitimas gali įvykti tik esant pakankami dideliam triukšmo lygiui. Dar vienas mūsų pasirinkimo privalumas - mes nenaudojame jokių adaptuotų prie duomenų slenksčių, o vieningą "slenkstį" - 0.


       

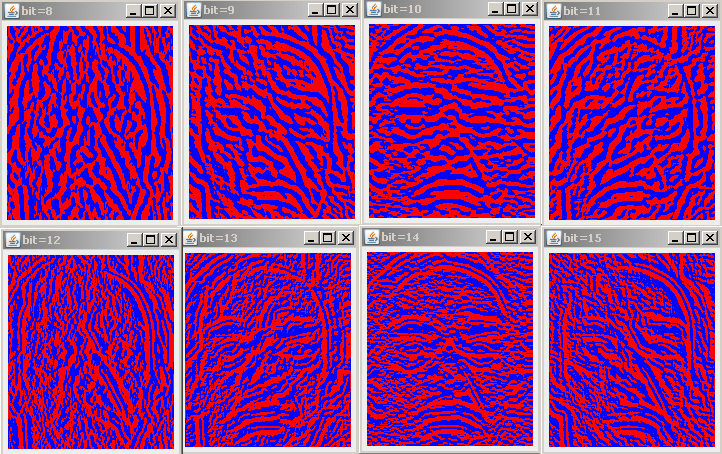
9 paveikslėlis. Veido binariniai požymiai.

9 pav. iliustruoja tokiu būdu gautus požymius. Raudona spalva žymi neneigiamas išvestines, mėlyna - neigiamas. Pirmosios eilutės iš kairės į dešinę einantys binarinių požymių vaizdai atitinka tokių išvestinių ženklus:

u(x+h,y+h) - u(x-h,y-h),   u(x+h,y) - u(x-h,y),  
u(x,y+h) - u(x,y-h),   u(x+h,y-h) - u(x-h,y+h).

Antrosios eilutės binarinių požymių vaizdai atitinka ženklus tų pačių išvestinių, skaičiuotų dviejų gretimų mastelių vidurkintų vaizdų skirtumams

Trečiosios eilutės iš kairės į dešinę einantys binarinių požymių vaizdai atitinka tokių išvestinių ženklus:

u(x+h,y) - 2 u(x,y) + u(x-h,y),   u(x+h,y+h) - 2 u(x,y) + u(x-h,y-h),
u(x,y+h) - 2 u(x,y) + u(x,y-h),   u(x+h,y-h) - 2 u(x,y) + u(x-h,y+h).

Ketvirtosios eilutės binarinių požymių vaizdai atitinka ženklus tų pačių kryptinių antrosios eilės išvestinių, skaičiuotų dviejų gretimų mastelių vidurkintų vaizdų skirtumams. Vaizdų vidurkinimo parametro σ konkrečių reikšmių nenurodome; jas pasirinkite laisvai vizualiai kontroliuodami gaunamų binarinių požymių vaizdus. Gaunami binariniai vaizdai turi būti ne perdaug chaotiški, nes tuomet lyginamos autentiškos veidų poros vaizdai turės menką panašumą. Taip pat binariniuose vaizduose neturi būti stambių vieno ženklo sričių, nes tuomet lyginama apsišaukėlių veidų pora atsitiktai stambių sričių dėka gali turėti didelę dalį sutampančių binarinių požymių. Iš pateiktų vaizdų matyti, kad antrosios eilės kryptinių išvestinių ženklai labiau varijuoja, nei pirmosios eilės kryptinių išvestinių. Didinant kryptinės išvestinės eilę vis dažniau skiriasi gretimų išvestinių ženklai, todėl lyginant tokius binarinius vaizdus vis sunkiau gauti reikšmingą sutapimą lyginamų autentintiškų veidų porų. Pateiktus požymius vadinsime Teiloro binariniais požymiais, nes jie gauti skleidžiant vidurkintą vaizdą lokaliai Teiloro eilute ir binariniai požymiai koduoja skleidinio pirmųjų koeficientų ženklus. Lyginant su Gaboro požymiais, pastarųjų naudojama žymiai mažiau. Taip yra dėl to, kad Gaboro požymiai santykinai lėtai apskaičiuojami ir todėl jie dažniausiai įvertinami išretintame taškelių tinklelyje. Turint pilnas binarinių požymių matricas galima aptikti smulkius lyginamų vaizdų poslinkius, tačiau kartu tai ilgina veidų palyginimo kaštus.

Binarinių požymių grupavimas

Lyginant dviejų šablonų binarinius požymius reikia apskaičiuoti sutampančių bitų kiekį. Binarinė xor operacija lygina dviejų skaičių bitus: sutampančiose bitų pozicijose įrašomas 0, o nesutampančiose 1. Dabartinės architektūros kompiuteriai xor operacijas gali atlikti su skaičiais užimančiais nuo vieno iki aūtuonių baitų. Deja nėra specifinės procedūros, kuri grąžintų skaičiaus dvejetainės išraiškos nulinių ar nenulinų bitų kiekį, todėl naudojamos iš anksto apdorotos lentelės (ang. lookup tables), kuriose saugojamas skaičiaus dominanančių nulinių bitų kiekis. Lentelės dydį apriboja atminties kaštai. Praktiškai įsitikinta, kad reikamos lentelėms atminties ir informacijos apdorojimų spartos optimumas pasiekiamas naudojant 16-os bitų lenteles. Tokią lentelę vadinsime ZeroBitsCount. Užrašysime keletą jos konkrečių reikšmių:

ZeroBitsCount[0] = 16,
ZeroBitsCount[1] = 15,
ZeroBitsCount[2] = 15,
ZeroBitsCount[3] = 14,
ZeroBitsCount[4] = 15,
... ,
ZeroBitsCount[0xffff-1] = 1,
ZeroBitsCount[0xffff] = 0.

Kad panaudoti tokią nulinių bitų skaitliukų lentelę, paskaičiuotus binarinius požymius reikia apjungtimi grupėmis. Pirma mintis būtų paprasčiausiai fiksuoti šablono taško (x,y) koordinates ir apjungti į short tipo (javos terminais) skaičių šešiolika skirtingomis kryptimis ir masteliais apskaičiuotų išvestinių binarinius (ženklo) požymius. Tačiau toks pasirinkimas grupuotų gana stipriai koreliuojančius požymius. Jei mastelių arba krypčių reikšmės yra artimos, tai tikėtina, kad išvestinių ženklai sutaps; tai ir apsprendžia koreliavimą. Lyginant koreliuojančius binarinių požymių rinkinius didėja tikimybė atsitiktinai gauti didelias panašumo reikšmes, o tai didina tikimybę apsišaukėliams prisirinkti daug panašumo taškų, kas blogina atpažinimo kokybę. Pavyzdžiui, kraštutinės koreliacijos atveju, galime gauti, kad fiksuotam taškui (x,y) abiejų šablonų visi 16-a bitų yra vienodi ( tarkime visos kryptinės išvestinės teigiamos ) ir tokiame taške gautume maksimalų bitų panašumą. Kad išvengti tokių atvejų, siūlome viename short tipo skaičiuje kaupti ne tos paties taško (x,y) binarinius požymius, o aplink jį esančių taškelių binarinius požymius.


10 paveikslėlis. Binarinių požymių sūkurio rinkinys.

10 pav. iliustruoja pasirenkamus taško aplinkos taškus. Centrinio taškelio (x,y) padėtis yra dviejų sūkurių pradžios taškas. Ir mėlynai ir juodai pažymėtuose sūkuriuose yra pasirenkama po 16-a taškelių. Mėlyno ir juodo sūkurių pradžios taškas įtraukiamas į abudu 16-os bitų rinkinius. Kad sūkurių pradžios taško binarinio požymio reikšmė nesikartotų abiejuose rinkiniuose, imami dviejų skirtingų mastelių ar krypčių išvestinių ženklai. Einant vieno sūkurio giją taip pat keičiamos mastelio (sigma) ir išvestinės krypties reikšmės. Konkrečių mastelių ir krypčių taisyklių nenurodome - galite laisvai pasirinkti patys. Renkantis parametrus stenkitės, kad taško aplinka būtų ne per daug išplitusi ir 16-os bitų rinkinio bitai būtų kuo mažiau koreliuojantys tarpusavyje.


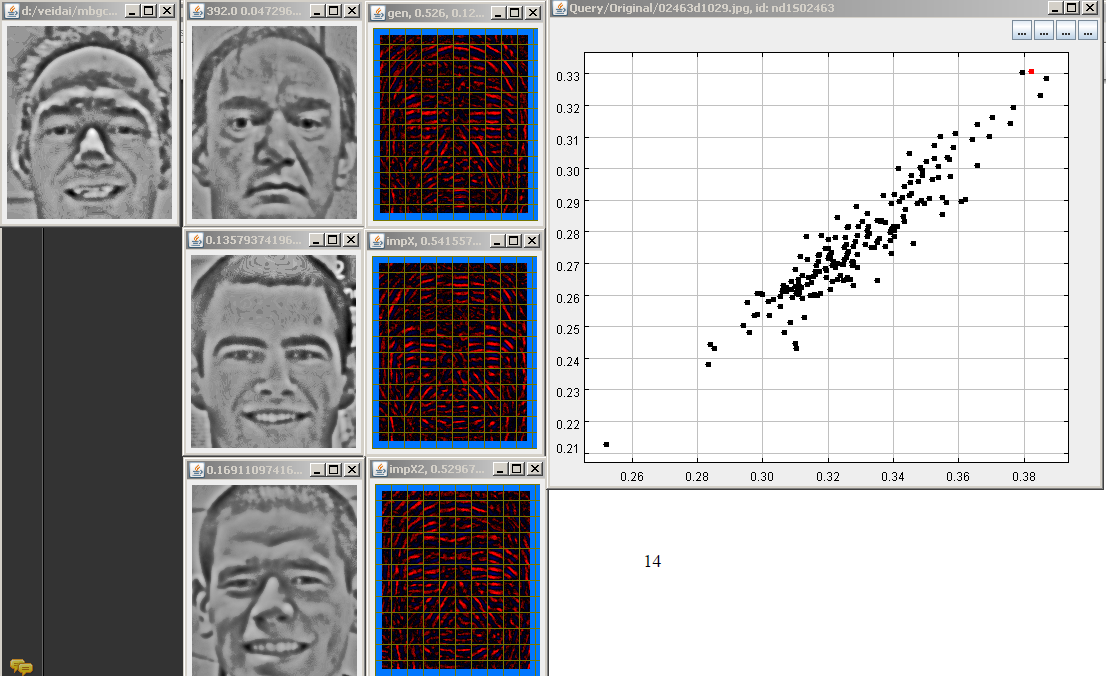
11 paveikslėlis. Panašumo metrikos derinimo aplinka.

Požymių palyginimas

Turint du požymių šablonus juos palyginti labai paprasta. Paprasčiausiai turite pasirinkti lyginimo centrų (x,y) tinklelį ir jo taškuose įvertinti panašumą. Panašumo metriką apibrėšime formule

ρ(Target,Query) = Σ(x,y) iš tinklelio ZeroBitsCount( TargetBitųRinkinys(x,y) XOR QueryBitųRinkinys(x,y)

Kad geriau būtų interpretuoti gautą panašumo reikšmę, ją galite normuoti. Normuojant reikia


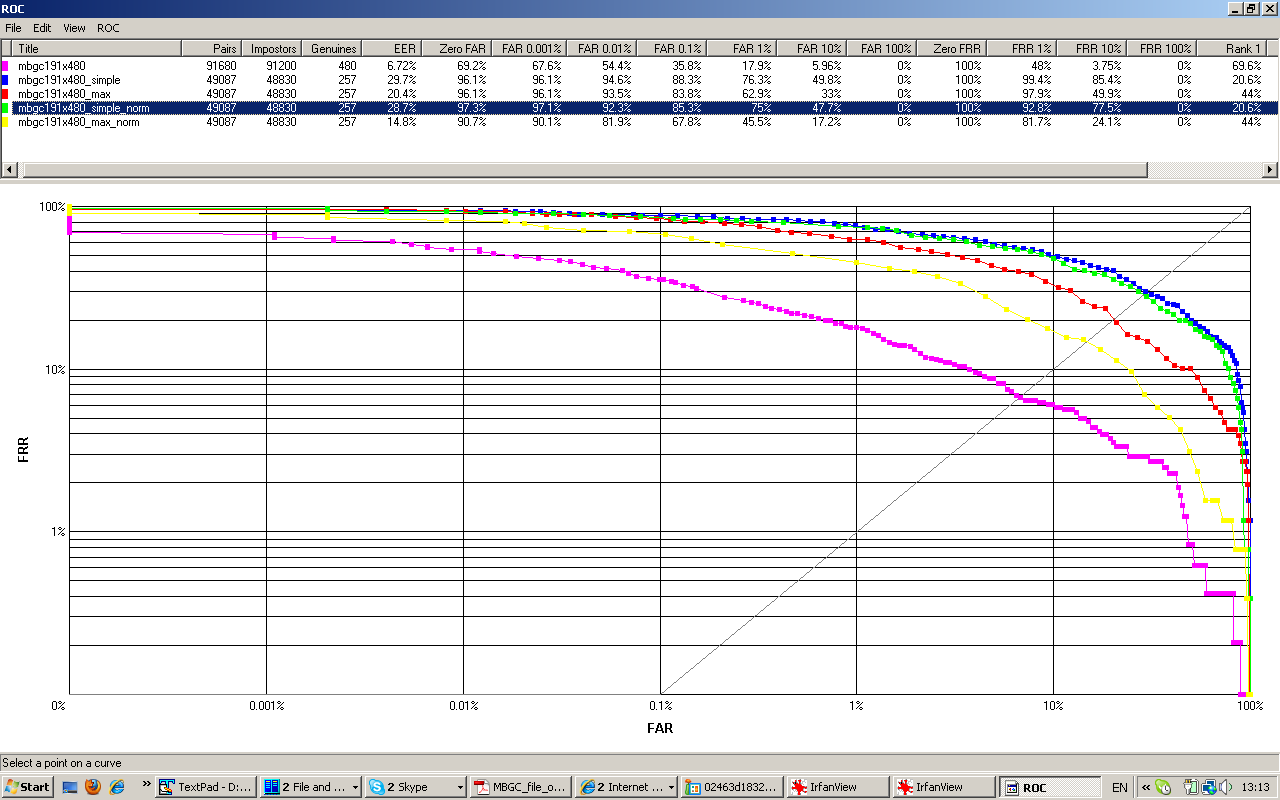
12 paveikslėlis. MBGC 191 Target ir 480 Query rinkinio įvairiosROC kreivės.

Tikėtinumo santykio logaritmas.

Lyginamų porų panašumo galimų reikšmių sritis priklauso nuo lyginimo metrikos. Tai apsunkina panašumo reikšmių interpretaciją. Tarkime jei vienos poros panašumo reikšmė yra $ρ = 0.8$, o kitos - $ρ = 0.65$, galime teigti, kad santykinai pirmosios poros veidai panašūs nei antrosios poros veidai, tačiau į kiekybinį klausimą "kiek kartų labiau panašūs" atsakyti negalima. Todėl biometrikoje vis dažniau taikomas {\em tikėtinumo santykio} ( angl. {\em Likelihood Ratio (LR)}) metrika, kurios reikšmes galima interpretuoti kiekybiškai. Lyginamos biometrijos poros $(X,Y)$ panašumo tikėtinumo santykis apibrėžiamas formule

LR(X,Y) = P{Tikėtinumas, kad lyginamos poros (X,Y) biometrikos sutampa } / P{ Tikėtinums, kad lyginamos poros (X,Y) biometrikos nesutampa }.

Bendrąja prasme tikėtinumas yra modelio tikimybė, kai žinomi atlikto eksperimento rezultatai. Mūsų atveju "eksperimento rezultatai" yra veidai $X$ ir $Y$ ir jų požymiai. Skaitiklio tikėtinumas yra kokio nors modelio tikimybė gauti ("išmatuoti") $X$ ir $Y$ veidų požymius, darant prielaidą, kad veidai yra to paties asmens, o vardiklio tikėtinumas yra tikimybė gauti tuos pačius $X$ ir $Y$ požymius, darant prielaidą, kad veidai yra skirtingų asmenų. Pagal apibrėžimą $LR$ reikšmės gali kisti nuo $0$ iki $∞$. Jei $0\le LR=LR(X,Y) < 1$, labiau tikėtina, kad lyginami veidai $X$ ir $Y$ yra skirtingi. Priešingai, jei $1 < LR < ∞$, labiau tikėtina, kad lyginami veidai sutampa. Kad išvengti intervalų $(0,1)$ ir $(1,∞)$ ilgių asimetrijos, dažnai vartotojui pateikiama $LR$ natūraliojo logaritmo reikšmė, kuri sutrumpintai žymima $LLR(X,Y) = LLR = \log(LR(X,Y))$ {\em (angl. Log Likelihood Ratio, LLR}). Jei tikėtinumo santykio logaritmas teigiamas, labiau tikėtina, kad lyginamos poros veidų pavyzdžiai yra vieno asmens. Priešingu atveju, kai tikėtinumo santykio logaritmas yra neigiamas, labiau tikėtina, kad tiriamos poros veidų pavyzdžiai priklauso skirtingiems asmenims. \caption{Tikėtinumo santykio LR ir jo natūraliojo logaritmo LLR reikšmės}
LR LLR Interpretacija
1000 6.9 Labai tikėtina, kad lyginami veidai sutampa
403.4 6 Labai tikėtina, kad lyginami veidai sutampa
100 4.6 Pakankamai tikėtina, kad lyginami veidai sutampa
20.1 3 Tikėtina, kad lyginami veidai sutampa
10 2.3 Labiau tikėtina, kad lyginami veidai sutampa
7.4 2 Labiau tikėtina, kad lyginami veidai sutampa
1 0 Vienodai tikėtina, kad lyginami veidai sutampa arba nesutampa
1/7.4 -2 Labiau tikėtina, kad lyginami veidai nesutampa
1/10 -2.3 Labiau tikėtina, kad lyginami veidai nesutampa
1/20.1 -3 Tikėtina, kad lyginami veidai nesutampa
1/100 -4.6 Pakankamai tikėtina, kad lyginami veidai nesutampa
1/403.4 -6 Labai tikėtina, kad lyginami veidai nesutampa
1/1000 -6.9 Labai tikėtina, kad lyginami veidai nesutampa

\ref{tab:LLRirLR} lentelėje pateiktos $LR$ ir $LLR$ reikšmės bei jų interpretacija. Pavyzdžiui, jei LLR = 6.9, tai apie 1000 kartų labiau tikėtina, kad lyginamojo ir tiriamojo veidų pavyzdžiai $X$ ir $Y$ priklauso vienam ir tam pačiam asmeniui nei skirtingiems ir atvirkščiai, jei LLR = -6.9, tai apie 1000 kartų labiau tikėtina, kad lyginamojo ir tiriamojo veidų pavyzdžiai priklauso skirtingiems asmenims nei tam pačiam asmeniui. Tikėtinumo santykiui įvertinti naudojami visi turimi lyginamieji veidų pavyzdžiai ir vieno tiriamųjų katalogo veidų pavyzdžiai. Todėl kuo lyginamųjų daugiau, tuo LLR patikimumas didesnis.

Kad pagal (\ref{LR}) apskaičiuoti tikėtinumo santykį $LR$, reikia įvertinti skaitiklio ir vardiklio reikšmes. Tikėtinumo reikšmės priklauso nuo pasirinkto modelio. Literatūroje modeliai dažnai konstruojami remiantis Gauso skirstiniu. Gauso skirstinys yra simetrinis ir su bet kokiais modelio parametrais modeliuojamas dydis gali įgyti bet kokias reikšmes iš intervalo $(-∞,∞)$. Tačiau mūsų atveju modeliuojamos panašumo reikšmės $ρ$ visuomet patenka į $[0,1]$ uždarą intervalą. Todėl mes modelio pagrindu pasirinkome eksponentinį skirstinį. Laikome, kad kiekvieno fiksuoto tiriamojo $X$ panašumo reikšmių tikėtinumai tenkina tokias lygtis:

P( ρ(X,Y) = s | \mbox{esant prielaidai, kad } X \mbox{ ir } Y \mbox{ yra vienodi}) = λ \exp(λ (s-a_X) )

ir

P( ρ(X,Y) = s | \mbox{esant prielaidai, kad } X \mbox{ ir } Y \mbox{ yra skirtingi}) = λ \exp(-λ (s-b_X) )

Laikome, kad ir skaitiklio ir vardiklio modelio parametras $λ$ yra vienodas. Šį parametrą galima įvertinti remiantis panašumo reikšmių dispersija, nes $1/λ^2$ yra eksponentinio skirstinio dispersija. Poslinkio parametrai $0 LR(X,Y) = λ \exp(λ (s-a_X) ) / (λ \exp(-λ (s-b_X)) = \exp(λ (2s-a_X-b_X))

ir

LLR(X,Y) = 2λ (s-(a_X+b_X)/2).

Aprašysime modelio parametrų $λ$, $a_X$ ir $b_X$ įvertinimo procedūrą.

{$λ$ parametro įvertis}

$1/λ^2$ parametro tikimybinė interpretacija yra veidų panašumo reikšmių dispersija skaičiuojant ją atskirai vienodiems ir skirtingiems veidams. Kadangi lyginamiems veidams turima tiksli informacija kokie veidai sutampa, o kokie skirtingi, $λ$ parametras įvertinamas naudojant tik lyginamųjų veidus $Y_1, Y_2, \cdots, Y_L$. Žymėjimų formulėse paprastumo dėlei laikysime, kad visi lyginamieji veidai $Y_1, Y_2, \cdots, Y_L$ yra skirtingų asmenų. Tuomet apskaičiuojame visus galimus $L^2-L$ skirtingų veidų panašumus: $$ ρ(Y_i,Y_j) = s_{i,j}, \ \ \ i, j = 1, \cdots, L, i \neq j. $$ Toliau kiekvienoje eilutėje $i$ išsirenkame $K = [\sqrt(L)]$ didžiausiųjų: $$ S_{i,k}, \ \ \ \ k=1,2,\cdots,K $$ ir dispersiją $1/λ^2$ įvertiname pagal įprastą dispersijos įverčio formulę: $$ 1/λ^2 = ∑i=1L( ∑k=1K Si,k2 - ( ∑k=1K Si,k )2 / K ) / (K-1) ) / L. $$

{$a_X$ ir $b_X$ parametrų įvertis}

$a_X$ ir $b_X$ ir parametrų įvertis priklauso nuo tiriamojo $X$ ir nuo to ar lyginami veidai taria {\em vienodą} ar {\em skirtingą} teksą (angl. {\em text dependent and text independent}). Tarkime lyginami veidai taria tą patį tekstą. Fiksuojame tiriamąjį veidą $X$ ir apskaičiuojame jo panašumą į visus lyginamuosius $Y_1, Y_2 \cdots Y_L$:

$$ s_1, s_2, \cdots , s_L \ \ \ (s_l = ρ(X,Y_l)). $$

Laikome kad didžiausias panašumas, t.y. $s^{max}=\max_{l}s_l$, priklauso vieno asmens lygintų veidų porai ir jį naudojame skaitiklio tikėtinumo modelio parametrui $a_X$ įvertinti, postuluojant, kad $a_X=s^{max}$. Laikome, kad antroji pagal dydį veidų poros panašumo reikšmė $s^{sec}=\max_{l}\{s_l \mbox{ išskyrus } s^{max}\}$ atitinka skirtingus asmenis ir ją naudojame apibrėžiant tikėtinumo santykio vardiklio eksponentinio skirstinio modelio parametrą $b_X$, postuluojant, kad $b_X = s^{sec}$.

Jei tariami tekstai yra skirtingi, aprašyta procedūra yra modifikuojama įvertinant $a_X$ dviejų dižiausiųjų panašumų aritmetiniu vidurkiu, o $b_X$ prilyginamas trečiajam pagal dydį panašumui.


Nuorodos

Naudingos nuorodos parinktos pagal veidų išskyrimo specialistą Robert Frischholz

NuorodaKomentarai
MetodikosVeidų išskyrimo populiariausių metodikų trumpi aprašymai
StraipsniaiVeidų išskyrimo rinktiniai straipsniai ir apžvalgos
DuomenysĮvairios veidų atpažinimo ir išskyrimo algoritmų testavimo duomenų bazės
Programinė įrangaNuorodos į laisvai platinimas ir komercines veidų išskyrimo bei atpažinimo sistemas
NuorodosVeidų išskyrimui skirtos nuorodos
SistemosVeidų atpažinimo sistemos
BendruomenėVeidų atpažinimo bendruomenė
KitaVeidų iliuzijos ir kita

Praktinis darbas

Realizuokite veidų atpažinimo algoritmą.
Jūsų sukurtas veidų išskyrimo algoritmas bus vertinamas pagal pateiktų algoritmui nežinomų veidų atpažinimo kokybę.

Reikalingų algoritmui atiderinti veidų pavyzdžius rasite čia. Algoritmas turi būti rašomas pratyboms skirtu laiku. Darbo turi būti atliekamas ir atsiskaitoma atskirais etapais.

  1. Pilnos nuotraukos ir akių pozicijų duomenų nuskaitymas, standartinio dydžio veido "iškirpimas".
    Atsiskaitoma pademonstruojant iškirptą veidą.
    Vertinama 0.7 egzamino balo.
  2. Perėjimas prie pilkumo lygmenų ir segmentuoto veido vidurkinimas dvimačiu simetriniu eksponentiniu filtru.
    Atsiskaitoma parodant pilkumo lygmenų ir vidurkintą vaizdą.
    Vertinama 0.7 balo.
  3. Vidurkinimas glodžiu eksponentinio tipo filtru ir normalizuoto veido apskaičiavimas.
    Atsiskaitoma pademonstruojant vidurkintą glodžiu eksponentiniu filtru veidą ir jo normalizuotą pilkumo lygmenų variantą.
    Vertinama 0.7 balo.
  4. Veido binarinių požymių apskaičiavimas.
    Atsiskaitoma pademonstruojant binarinių požymių vaizdus pasirinktoje skalėje.
    Vertinama 0.7 balo.
  5. Veidų binarinių požymių palyginimas. Palyginimui naudokite sūkurių binarinių požymių rinkinį ir paprasčiausią panašumo metriką.
    Palyginkite visas galimas Target ir Query veidų poras, pasirinktų Target ir Query yra nedideli (iki 20 ) mbgc veidų aibės poaibiai.
    Atsiskaitoma parodant ROC kreivę.
    Tema užskaitoma, jei gautos ROC kreivės EER (lygios klaidos tikimybė ) nedidesnė kaip 30%.
    Vertinama 0.7 balo.
  6. Veidų verifikacijos konkursas.
    Paruoškite veidų verifikacijos algoritmą, kuris apskaičiuotų duotų mokymo (target.list) ir testavimo (query.list) sąrašų porų panašumus.
    Jūsų algoritmai bus testuojami su naujais MBGC veidų duomenimis.
    Skaičiavimams turite perduoti dėstytojui algoritmus paruoštus tokiu būdu.
    • Jūsų vykdomasis "*.exe" arba java "*.jar" failas (Matlab, Python ir kitos programavimo terpės neturi būti naudojamos) turi būti paleidžiamas komandine eilute, kurioje papildomai nurodomi du parametrai: target.list ir query.list.
      Tarkime, jei jūsų programos vardas ManoVeido.jar, naudojimo pavyzdys būtų

      java -Xmx1024m -jar ManoVeido.jar mbgcBigTarget.list mbgcQuery.list

    • Jūsų programa turi kiekvieną fiksuotą Query sąrašo elementą
      (pvz. F:/mbgc/data/StillChallenge/Query/Original/02463d1006.jpg ) sulyginti su visais target.list sąrašo elementais ir gautus rezultatus įrašyti į *.roc formato failą.
      Pavyzdžiui mbgcBigTarget.list ir mbgcQuery.list sąrašuose yra 20 target ir 19 query paveiksliukų. Todėl į ManoVeido.roc failo pirmuosius keturis baitus įrašote 20x19 = 380 sveikąjį skaičių (binarine forma).
      Į sekančius keturis baitus įrašote 0 - target sąrašo pirmojo failo numerį.
      Sekančiuose keturiuose baituose įrašote taip pat 0 - query sąrašo pirmąjį numerį.
      Kituose keturiuose baituose įrašote 1 (genuines/autentiška pora), nes ID(02463d634.png) = 02463 == ID(02463d1006.jpg) = 02463 ( veido ID yra penki skaitmenys stovintys prieš failo pavadinimo "d" raidę, po "d" nurodomas filmavimo sesijos/kadro numeris, kuris *.roc įrašų neįtakoja).
      Kiti keturi ManoVeido.roc failo baitai patys svarbiausi - juose įrašote jūsų programa apskaičiuotą
      similarity(02463d634.png,02463d1006.jpg) Sekančiame keturių baitų ketvertuke pasikeis target įrašo numeris (jis bus lygus 1 ), genuine/impostors reikšmė bus 0, nes
      ID(04201d429.png) = 04201 != ID(02463d1006.jpg) = 02463 ir taip pat tikėtina, kad gausite mažesnę similarity(04201d429.png,02463d1006.jpg) reikšmę.
      Tęsiant tolimesnius skaičiavimus, atkreipkite dėmesį, kad query įrašų indeksai kinta ne po vienetą o sparčiau (tas pats gali būti ir target sąrašo elementams). Tokiu atveju į roc failą įrašote iš *.list failų nuskaitytas reikšmes.
    • Kad jūsų programa sugebėtų palyginti pakankamai daug porų, jai keliami veidų poros palyginimo spartos reikalavimai.
      Skaičiavimai bus atliekami su Intel Core 2 Duo, 2.1 GHz, 2 Gb Ram PC.
      Programa turi palyginti bent 100 veidų porų per sekundę.
      Kad pagreitinti skaičiavimus, rekomenduotina pirma apskaičiuoti požymių šablonų target ir query bazes. Rekomenduojama ekrane atspausdinti informaciją, kad kuriami palyginimui reikalingi šablonai. Maksimalus vieno šablono sukūrimo laikas 1 sek.
    • Pilnai paruošta programa vykdymui kartu su programų pradiniais kodais turi būti pateikta iki 2009 gruodžio 16 d. (imtinai).
    • Vertinama 1 balo už atitinkančius reikalavimus algoritmo pateikimą.
      Papildomai, priklausomai nuo algoritmu gautų rezultatų, skiriama iki penkių konkursinių egzamino balų, kurie atsikirai prisideda prie jūsų pratybų ir teorijos balų.
      Kiekvienam algoritmui gavusiam mažiausią
      • EER
      • ZeroFAR
      • FRR @ FAR1%
      skiriamas maksimalus įvertinimas: 5-i konkursiniai balai.
      Skiriamų balų kiekis už kitas vietas priklausys nuo dalyvių skaičiaus ir rezultatų artumo iki geriausiojo.

Literatūra

  1. Wikipedija. Bitiesinė interpoliacija.
  2. [GW2002] R. Gonzalez, R. Woods, “Digital Image Processing” Prentice Hall, Second ed., 2002.
  3. [VP2005] Villegas, M., Paredes, R.: Comparison of illumination normalization methods for face recognition. In: Third COST 275 Workshop - Biometrics on the Internet, University of Hertfordshire, UK (October 2005) 27–30.
  4. [VP2007] M. Villegas and R. Paredes. "Illumination Invariance for Local Feature Face Recognition". 1st Spanish Workshop on Biometrics, SWB2007.
  5. Paul Viola and Michael J. Jones. Rapid Object Detection using a Boosted Cascade of Simple Features. IEEE CVPR, 2001
  6. O. Jesorsky, K.J. Kirchberg, and R.W. Frishholz. Robust Face Detection Using the Hausdorff Distance. InProc. Third International Conference on Audio- and Video - based Biometric Person Authentication, Springer, Lecture Notes in Computer Science, LNCS-209ą, pp. 90-95, Halmstad, Sweden, 6-8 June 2001.
  7. Rainer Lienhart, Alexander Kuranov, and Vadim Pisarevsky. Empirical Analysis of Detection Cascades of Boosted Classifiers for Rapid Object Detection. MRL Technical Report, Intel Labs, May 2002, revised Dec. 2002. [PDF]
  8. Yoav Freud and Robert E. Schapire. A decision-thepretic generalization of online learning and an application boosting. In Computational Learning Theory: Eurocolt '95, pages 23-37. Springer-Verlang, 1995.
  9. Akių judesiai stebint paveikslą
  10. M.P. Dubuisson and A.K. Jain. A modified Hausdorf distance for object matching. In ICPR94, pages A:566-568, Jerusalem, Israel, 1994.
  11. D.A. Forsyth slaidai. Templatematching

Past. Prašau informuoti apie pastebėtus netikslumus algirdas.bastys@maf.vu.lt

2009 m. rugsėjo 21 d.