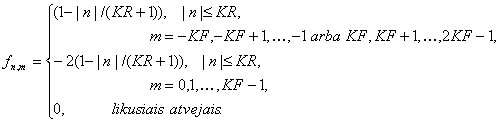Rainelės atpažinimas
A.Bastys
Įvadas. Rainelė yra turtingos tekstūros žiedo formos matoma akies dalis tarp vyzdžio ir stiklakūnio ( žiūr. 1 pav.). 1936 m. oftalmologas ( akių ligų specialistas ) Frank Burch
suformulavo mintį apie akių rainelių panaudojimą asmens identifikavimui. Pereito amžiaus 8-ajame dešimtmetyje akies rainelės panaudojimo identifikacijai idėja pasirodė James Bond seriale, tačiau praktiškai ji dar nebuvo realizuota.1987 m. du oftalmologai Aran Safir ir Leonard Flom užpatentavo šią idėją ir 1989 m. jie paprašė John Daugman ( Harvardo universiteto lektoriaus ) sukurti tinkantį kompiuteriui akių rainelių atpažinimo algoritmą. Daugmano pradinis algoritmas aprašytas [Daugman, 1993] straipsnyje. Šiuolaikinės komercinės rainelių atpažinimo sistemos naudoja įvairias originalaus Daugman algoritmo modifikacijas, tačiau principinė atpažinimo schema nesikeičia. Teises į patentus išpirko Iridian Technologies [Iridian Technologies] kompanija ir sėkmingai vysto asmenų identifikavimo pagal akies rainelę biznį.
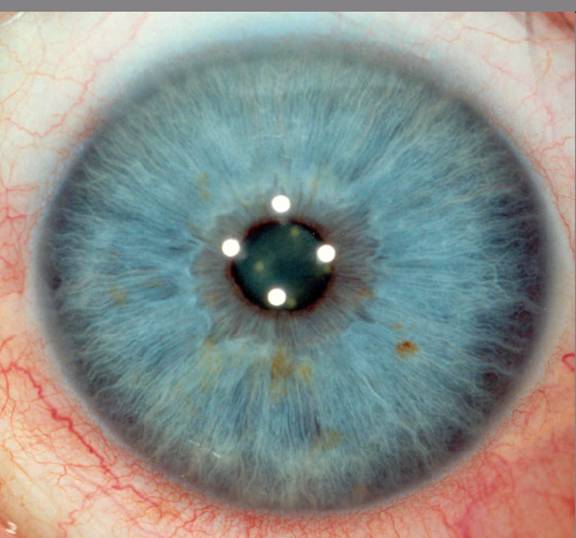
1 pav. Žmogaus akies rainelės spalvota nuotrauka.
Privalumai. [Wikipedia, Iris recognition] Akies rainelės panaudojimas biometrikoje turi daug privalumų.
- Rainelė gerai apsaugota nuo išorinio poveikio labai skaidria membrana. Palyginimui pirštų atspaudai nuolat kinta nuo ranka laikomos cigaretės sukeltų mikro-nudeginimų, įsipjovimų peiliu, mechaninio poveikio dirbant rankomis.
- Rainelė iš esmės yra plokščia ir jos geometrija keičiama tik dviem nepriklausomais raumenimis reguliuojančiais vyzdžio skersmenį. Tai sąlygoja rainelės pastovumą lyginant pavyzdžiui su trimačio veido projekcijomis.
- Rainelės turi turtingą unikalią tekstūrą, kuri, panašiai kaip ir pirštų atspaudai, atsitiktinai suformuojama embriono vystymosi stadijoje. Net genetiškai identiški dvyniai turi nepriklausomas rainelių tekstūras. Palyginimui pasaulyje yra apie 10 milijonų genetiškai identiškų dvynių, kurių DNR negali būti panaudota jų identifikacijai.
- Rainelės skenavimo procedūra analogiška paprastam fotografavimui atliekamą nuo 10 cm. iki kelių metrų atstumu. Tai žymiai maloniau, nei pavyzdžiui liesti pirštų atspaudų skenavimo mechanizmą, kurį, gal būt, ką tik lietė kitas jums nežinomos higienos kultūros asmuo.
- Yra publikacijų teigiančių, kad apie 200 taškelių akies rainelės skersmens vaizdas yra žymiai informatyvesnis nei pirštų atspaudų vaizdas.
- Šiuo metu komercinis John Daugman IrisCode
algoritmas pasižymi unikaliu FAR (angl. False Acceptance Rate )
rodikliu geresniu nei
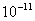 . Atlikus daugiau kaip 200 milijardų
palyginimų naudojant realius Jungtinių Arabų Emiratų imigracijos kontrolės
sistemoje sukauptus duomenis [Daugman techreport 635] nebuvo nei vieno false
acceptance atvejo.
. Atlikus daugiau kaip 200 milijardų
palyginimų naudojant realius Jungtinių Arabų Emiratų imigracijos kontrolės
sistemoje sukauptus duomenis [Daugman techreport 635] nebuvo nei vieno false
acceptance atvejo. - Nors ir egzistuoja medicininės ir techninės procedūros dalinai keičiančios rainės spalvas ir geometriją, tekstūra iš esmės lieka stabili dešimtmečiais. Yra pavyzdžių sėkmingos rainelių identifikacijos 30 metų laikotarpiu.
Trūkumai.
- Rainelių skenavimas yra santykinai jauna technologija ir negali lygintis su analogiškomis pirštų atspaudų duomenų saugyklomis.
- Identifikuoti rainelę labai keblu didesniu nei keli metrai atstumu ir tuo atveju, kai identifikuojamas asmuo nekooperuoja su sistema nukreipdamas galvą nuo kameros.
- Kaip ir kitos biometrinės sistemos rainelių biometrinė identifikacijos sistema jautri blogos kokybės vaizdams.
- Kaip ir kitų biometrinių identifikavimo sistemų atveju, prieš rainelių duomenų bazių kaupimą pasisako kovos už asmenų teises organizacijos.
- Skirtingai nuo pirštų atspaudų, kol kas nemokama išgauti rainelių vaizdų kopijas paliktas nusikaltimų vietose.
Praktiniai taikymai.
Tarptautinė civilių skrydžių organizacija [ICAO] akies raineles, kartu su pirštų atspaudais ir veidais, pripažino ir standartizavo ateities pasų panaudojime. Olandijos Schiphol aerouoste naudojama imigracijos tarnyboje nuo 2001 metų [Schiphol]. Jungtinių Arabų Emiratų visuose 17 oro, sausumos ir jūros pasienio kontrolės punktuose naudojama akies rainelės atpažinimo procedūra taip pat nuo 2001 metų [UAE]. [UK IRIS] Anglijoje funkcionuoja IRIS Iris Recognition Immigration System. Keletas Kanados aerouostų taip pat naudoja rainelės atpažinimą skrydžių saugumo kontrolės tikslais.
Rainelės atpažinimo schema.
Bendra rainelės atpažinimo schema nesiskiria nuo įprastinės vaizdų atpažinimo schemos. Galima sudaryti tokią atpažinimo blokinė schemą:
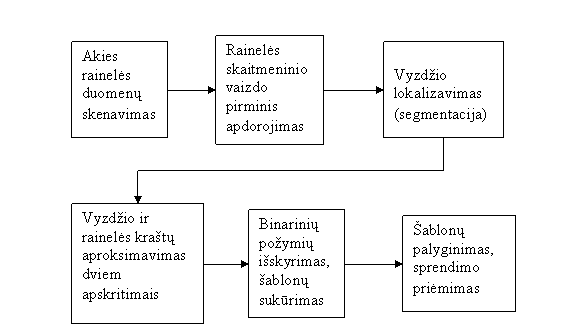
2 pav. Akies rainelės atpažinimo schema.
Aptarsime kiekvieną rainelės atpažinimo blokinės schemos elementą atskirai.
Akies rainelės duomenų skenavimas.
Akies rainelės duomenų skenavimas įskaitmenina rainelės analoginį ( realų ) vaizdą. Duomenų atpažinimui pateikimą skaitmenine forma sąlygoja šiuolaikinių kompiuterių architektūra. Kadangi spalvinė rainelių informacija mažiau atspari laikui ir medicininėms
Priemonėms, spalvinė rainelių informacija šiuo metu komercinėse atpažinimo sistemose nenaudojama. 3 pav. pateiktas vienas nespalvotos rainelės nuotraukos pavyzdys. Atkreipkite dėmesį į ryškią baltą dėmę vyzdžio srityje ( 23 val. kryptimi ). Tokios dėmės kaip taisyklė matomos skaitmeninėse rainelių nuotraukose ir gaunasi dėl specifinio apšvietimo šaltinio išryškinančio infraraudonąsias elektromagnetines vaizdo bangas. Kitas skenavimo būdo sąlygotas defektas yra taip vadinamas interlacing [Interlacing], kuris pasireiškia lyginių ir nelyginių vaizdo eilučių pasislinkimu, kuris atsiranda dėl skenavimo pirma lyginių, o po to nelyginių vaizdo eilučių.
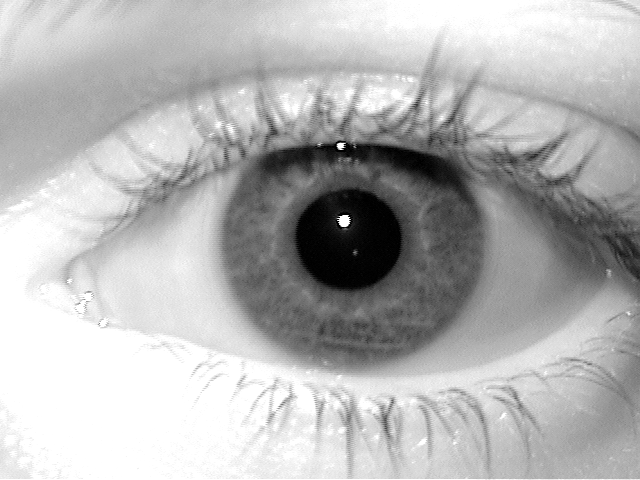
3 pav. NIST ICE 2005 rainelių duomenų bazės 242116.tiff failo rainelės vaizdas.
Rainelės vaizdo pirminis apdorojimas. Pirminis rainelės vaizdo apdorojimas, kaip ir kitais vaizdų atpažinimo atvejais, yra mažiausiai standartizuotas. Mes naudodami pirminį vaizdo apdorojimą spręsime tris problemas.
- Eliminuosime vaizdo kokybės pablogėjimą sąlygotą interlacing [Interlacing] efekto.
- Pašalinsime apšvietimo šaltinio sąlygotus ryškius atšvaitus.
- Apskaičiuosime kaupiamąjį vaizdą [IntegralI mage], kuris bus naudingas lokalizuojant vyzdį vaizde.
Egzistuoja daug ir gana sudėtingų interlacing efekto sukeltų vaizdo iškraipymo problemos sprendimų. Vienas jų yra paprastas ir siūlo eliminuoti kas antrą (pavyzdžiui nelyginę) vaizdo eilutę. Kadangi mums svarbu išsaugoti apskritiminę rainelės simetriją mes eliminuosime ne tik nelygines vaizdo eilutes bet ir nelyginius vaizdo stulpelius. Kadangi rainelės nuotraukos kokybės būna aukštos rezoliucijos, sumažintas du kartus imčių skaičius horizontalia ir vertikalia kryptimis išsaugos gana detalią informaciją apie rainelės tekstūrą ir tuo pačiu apie 4 kartus paspartins vėlesnius skaičiavimus atliekamus su vaizdo taškelių matrica. Atlikus šią parastą deinterlacing procedūrą gausime tokį vaizdelį:
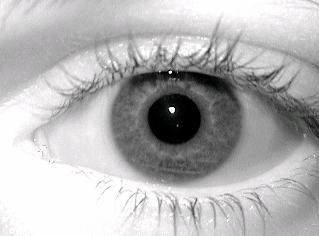
4 pav. 242116 vaizdas, kuriame eliminuotas lyginių/nelyginių eilučių triukšmas..
Pradiniame vaizdelyje interlacing iškraipymai lengvai pastebimi balto atšvaito bei atskirų blakstienų srityje. 4 pav. vaizdo kokybė šia prasme yra geresnė. Sumažintos rezoliucijos vaizde rainelės tekstūra išlieka pakankamai aiški, kad remiantis ja būtų galima identifikuoti skirtingas raineles.
Baltus apšvietimo atšvaitus pašalinsime tokiu būdu. Pirma pasirinksime šviesumo slenkstį trshld (pvz. trshld = 220 ). Tuomet surandame jungią taškų (x,y) sritį vaizde, kurioms vaizdo reikšmės image(x,y) > trshld. Fiksuojame kokią nors tokių taškų sritį ir užpildome jos reikšmes srities krašto vaizdo reikšmių vidurkiu. Atlikę šias procedūras gauname 5 pav. rainelės vaizdą.
Kaupiamasis vaizdas IntegralImage(x,y) gaunamas susumuojant visas image(i,j) reikšmes, kur (i,j) koordinatės tenkina sąlygas i <= x ir j <= y. Šio vaizdo nevizualizuosime, nes kaupiamasis vaizdas skirtas ne vizualizacijai, o yra pagalbinė priemonė greitų vaizdo vidurkių bet kokiame stačiakampyje apskaičiavimui kuo mes vėliau ir pasinaudosime. Plačiau apie kaupiamąjį vaizdą galite paskaityti [Integral Image] šaltinyje.
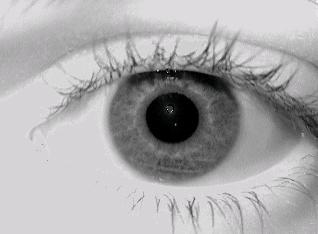
5 pav. Rainelės vaizdas pašalinus didelio intensyvumo sritis.
Vyzdžio lokalizavimas.
Objekto lokalizacija yra sudedamoji daugelio vaizdų atpažinimo algoritmų dalis. Lokalizuojant kokį nors objektą reikia surasti sritį ar sritis vaizde kuriose yra mus dominantis objektas nekreipiant dėmesio į individualias objekto detales pagal kurias vėliau yra identifikuojamas konkretus objektas. Java programavimo terminais lokalizuojant reikia atpažinti Java klasės tipą, o atpažinimas ekvivalentus kokio nors klasės konkretaus egzemplioriaus identifikavimui. Rainelės atveju patogiau pradžioje lokalizuoti ne visą rainelę, o tik sritį vaizde, kuri atitinka vyzdį. Užpildžius baltus atšvaitus, vyzdys pasižymi mažo intensyvumo image(x,y) reikšmėmis. Tačiau blakstienos, ypač merginų, kurios specialiai ryškina jas juodu tušu, taip pat pasižymi mažomis intensyvumo reikšmėmis. Kadangi blakstienos yra nedidelio storio vidurkintame vaizde blakstienas atitinkančios reikšmės vidurkinsis su gretimomis didesnėmis veido spalvos reikšmėmis, o vyzdžio vidurio taškai išliks tokie pat tamsūs. Kad greitai atlikti vidurkinimo operaciją patogu naudoti kaupiamąjį vaizdą. Stačiakampyje, kurio viršūnės taškuose (a-1,b-1) ir (c,d), ( a<c, b<d) esančių vaizdo reikšmių image(x,y) suma yra lygi
IntegralImage(c,d) - IntegralImage(a,d) - IntegralImage(c,b) + IntegralImage(a,b);
Vadinasi šio stačiakampio vidutinė vaizdo reikšmė bus randama keletu sudėties/atimties bei daugybos/dalybos veiksmais:
Mean( image )_( (c,d)x(a-1,b-1) ) = (IntegralImage(c,d) - IntegralImage(a,d) - IntegralImage(c,b) + IntegralImage(a,b)) / ((c-a)(d-b));
Kad vidurkintas vaizdas būtų labiau lokalizuotas mes vidurkiname du vidurkintus vaizdus, kurių stačiakampiai lokalizuoti arba horizontalia arba vertikalia kryptimi. Galutinė vidurkinto vaizdo reikšmė taške (x,y) apskaičiuojama formule
Mean(image)(x,y) = 0.5 *(Mean(image)_((x+1, y+h), (x-1-1, y-h-1)) + Mean(image)_((x+h, y+1), (x-h-1, y-1-1))).
Čia h yra vidurkinimo stačiakampio didžiosios kraštinės pusė.
6 pav. iliustruoja gaunamą vidurkinimo rezultatą ( h = 10 ).

6 pav. 20x20 kvadratuose vidurkintas rainelės vaizdas.
Detektuojant vyzdį vaizde yra ieškomas globalus vidurkinto vaizdo minimumas
argMin( Mean(image)(x,y) ) = (x_min, y_min)
ir surandama jungi taškų sritis, kurios elementai (x,y) tenkina sąlygą
Mean(image)(x,y) >= Mean(image)(x_min,y_min) + delta.
Slenksčio reikšmė delta parenkama eksperimentiniu būdu ir 256 pilkumo lygių vaizde tipinė reikšmės yra delta = 8, 16 arba 32.
7 pav. iliustruoja gaunamo vyzdžio lokalizacijos rezultatą. Rausvais taškais pažymėtas išskirtos jungios vyzdžio srities kraštas. Šiuo atveju delta reikšmė buvo 32.
Suradus akies vyzdžio sritį randamas šios srities taškų koordinačių aritmetinis vidurkis. 7 pav. taškas su aritmetinio vidurkio koordinatėmis pažymėtas mažu raudonu kryžiuku. Taip pat apytiksliai įvertinamas vyzdžio spindulys, kurio reikšmė randama apskaičiuojant atstumų vidurkį tarp išorinio vyzdžio kontūro taškų ir rasto vyzdžio centro. 7 pav. pavaizduotos akies atveju gaunama vyzdžio spindulio reikšmė yra apytiksliai lygi 28 taškeliams.
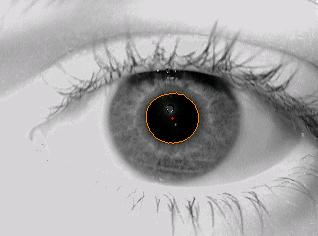
7 pav. Lokalizuoto vyzdžio vaizdas. Rausvi taškai žymi vyzdžio srities kraštinius taškus, raudonas vyzdžio srities taškų koordinačių aritmetinį vidurkį.
Vyzdžio ir rainelės kraštų aproksimavimas dviems apskritimais.
Sekačiame etape yra patikslinamas vyzdžio centras bei jo kraštą aproksimuojantis apskritimas ir surandamas analogiškas apskritimas rainelės išoriniam kraštui. Kad išryškinti kraštus dažnai naudojamas diferencijavimas. Vieno kintamojo funkcijos pirmosios eilės išvestinė greito reikšmių kilimo srityje turės lokalų maksimumą, o greito kritimo srityje minimumą. Antrosios eilės išvestinė ir maksimumo ir minimumo taškų aplinkose kirs nulinę reikšmė. Dažniausiai tokie taškai ir yra naudojami detektuoti kraštams. Mūsų atveju patogu naudoti jau detektuotą vyzdžio centrą nustatyti krypčiai kuria yra skaičiuojama antrosios eilės išvestinė. Tiksliau antrosios eilės išvestinė yra aproksimuojama antrosios eilės skirtumais spindulio išvesto iš vyzdžio centro kryptimi. Tokiu būdu vaizdo image(x,y) antrosios eilės diferencialas spindulio kryptimi randamas pagal formulę
Diff_rr(image(x,y)) = image( xo + (r + dr ) cos(fi), yo + (r + dr ) sin(fi) )
2 image( xo + r cos(fi), yo + r sin(fi) ) +
image( xo + (r - dr ) cos(fi), yo + (r - dr ) sin(fi) ).
Čia (r, fi ) yra (x,y) taško polinės koordinatės randamos iš lygčių
x = xo + r cos(fi),
y = yo + r sin(fi),
(xo,yo) yra detektuoto vyzdžio centro koordinatės, o dr diferencialo žingsnis, kurio praktinė reikšmė gali būti apie 5 taškelius. Įstačius konkrečias reikšmes daugeliu atvejų gausime nesveikaskaites vaizdo koordinates. Todėl tenka vaizdo reikšmes bitiesiškai interpoliuoti panaudojant 4-ias vaizdo reikšmes artimiausiose sveikaskaitėse koordinatėse (plačiau žiūr. [Bilinear Interpolation]). Kad neskaičiuoti be reikalo stipriai nutolusiuose nuo vyzdžio centro vaizdo taškuose diferencialų galima apsiriboti maksimalaus rainelės spindulio skrituliu. Kadangi dažnai į rainelės sritį patenka apatinis ir viršutinis akies vokas taip pat tikslingas apsiriboti tik 45 laipsnių sektoriais išeinančiais iš vyzdžio centro, kurių simetrijos ašis yra lygiagreti horizonto linijai. 8 pav. iliustruoja apskaičiuotas nurodytoje srityje antrosios eilės diferencialo reikšmes. Kuo spalva raudonesnė tuo didesnė diferencialo teigiama reikšmė pažymėtame taške, kuo spalva mėlynesnė tuo reikšmė didesnė neigiama, reikšmės artimos nuliui arba kurios neskaičiuotos nuspalvintos juodai. Balta spalva žymi perėjimo iš mėlynos spalvos į raudoną taškus ( t.y. antrosios eilės diferencialo spindulio kryptimi nulio kirtimo taškus, o geltona analogiškus taškus kai spalva žiūrint iš kairės į dešinę iš raudonos pereina į mėlyną. Kad greitai ir tiksliai įvertinti apskritimų ribojančių vyzdžio ir rainelės kraštus sudaroma nulio kirtimo taškų nuotolių iki vyzdžio centro histograma. Histograma skaičiuojama atskirai kiekvienam jungiam nulio kirtimų kontūrui. Gautas histogramas taip pat galima kiek pavidurkinti, kad jų grafikai būtų tolydesni.

8 pav. Antrosios eilės diferencialai apskaičiuoti riboto apskritimo ilgio 45 laipsnių sektorių, išeinančių iš vyzdžio centro, srityse.
9 pav. iliustruoja gaunamas histogramas. Dvi beveik susiliejančios histogramos turi maksimumus atitinkančius argumento reikšmes 55 ir 56. Šios histogramos atitinka kairįjį ir dešinįjį vyzdžio kontūrą, o maksimumai atitinka vyzdį aproksimuojančio apskritimo spindulį. Prisiminkime, kad pradinė įvertinta apskritimo reikšmė buvo lygi 28. Beveik dvigubas spindulio padidėjimas gavosi todėl, kad pereidami prie polinių koordinačių mes pasmulkinome du kartus skaičiuojamų taškų mastelį kad gauti tikslesnes vyzdžio ir rainelės kraštus ribojančių apskritimų reikšmes. Kitų dviejų reikšmingų histogramų grafikų maksimumai yra dešiniau ir jų reikšmės yra 130 ir 136. Šios dvi histogramos atitinka rainelės dešinio ir kairiojo išorinio krašto kontūrus, o jų maksimumai rainelės kraštus aproksimuojančių apskritimų spindulius. Šiuo atveju gautų spindulių reikšmės skiriasi gana daug, tiksliau 136 130 = 6 taškeliais. To priežastis yra ta, kad vyzdžio centras netiksliai sutampa su rainelę ribojančio apskritimo centru. Todėl papildomai apjungiame atskirai taškus sudarančius du kontūrus ( kairįjį ir dešinįjį ), kurie riboja vyzdį, bei taškai analogiška rainelės kraštų kontūrų taškų aibė. Šioms dvejoms taškų aibėms surandami du apskritimai minimizuojantys atstumus kontūrų taškų iki apskritimų. Į šių apskritimų apskaičiavimo detales nesigilinsime, pažymėsime tik kad gaunamų apskritimų centrai ir spinduliai ir yra galutinis segmentacijos/lokalizacijos rezultatas.
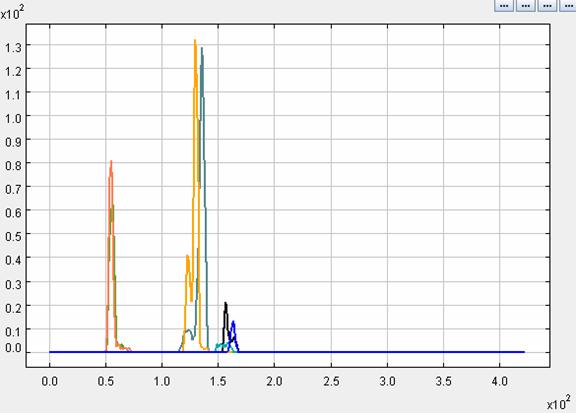
9 pav. Jungių kontūrų taškų atstumų iki vyzdžio centro histogramos.
10 pav. iliustruoja galutinį rainelės lokalizacijos algoritmo darbo rezultatą. Žaliasis apskritimas ir jo centro taškas aproksimuoja akies vyzdį ribojantį kontūrą, kuris sutampa su rainelės vidiniu kontūru, o geltonai nuspalvintas apskritimas ir centro taškas žymi rainelės išorinio krašto kontūrą aproksimuojantį apskritimą. Originalus Daugman ir kiti algoritmai papildomai dar detektuoja apatinį ir viršutinį voką aproksimuojančius apskritimus. Kadangi šiems apskritimams išskirti netinka histograma sudaryta iš kontūro taškų atstumų iki vyzdžio centro, šiuo atveju reikėtų taikyti apskritiminę Hough transformaciją [Circular Hough Transform]. Hough transformacijos sudėtingumas yra žymiai sudėtingesnis, nes ieškomas ne vienas parametras apskritimo spindulys, bet dar papildomi du centro taško koordinatės, todėl mes savo algoritme jo nenaudojame. Būsiu dėkingas, jei kas pasiūlysite greitus ir patikimus algoritmus akių vokų kraštams surasti. Čia aprašytas algoritmas yra realizuotas Java kalba ir vienam 3 pav. pateiktos rezoliucijos vaizde lokalizuoja rainelę vidutiniškai per 0.25 sek. ( 2.8 GHZ PC).

10 pav. Vyzdį ir akies rainelės išorinė kontūrą aproksimuojantys apskritimai.
Binarinių požymių išskyrimas
Atlikus segmentaciją atsiranda galimybė išskirti požymius. Apskaičiuodami požymius remsimės Daugman tradicija, t.y. rainelės požymiai bus binarinių skaičių, t.y. 0/1, matrica. Tokia binarinių požymių patogi palyginimui nes galima apjungti 0/1 grupėmis, pvz. po 16 pozicijų ir lyginimo metu operuoti su tomis grupėmis, kas žymiai pagreitina skaičiavimus. Originaliame Daugmas darbe yra naudojami Gaboro filtrai [Gabor filter]. Mes naudosime paprastesnius filtrus, kurių esmė išlieka tapati filtrų svoriai parenkami taip, kad jie trivialius signalus, pvz. konstantą atvaizduotų į nulį ir konkreti požymio reikšmė parenkama pagal filtravimo rezultato ženklą.
Pradžioje reikia nuspręsti kokį signalą filtruosime. Atlikę rainelės segmentaciją gauname du apskritimus, kurių mažasis aproksimuoja kontūrą ribojantį vyzdį ir vidinį rainelės kraštą, o didysis aproksimuoja išorinį rainelės kontūrą. Pradžioje tarkime paprastumo dėlei, kad šių dviejų apskritimų centrai sutampa. Tuomet išskirta rainelė sudaro žiedą, ribojamą R_pupil ir R_iris spinduliais. Daugman schemoje požymiams išskirti yra pereinama prie vaizdo polinių koordinačių sistemos, kurios centras sutampa su išskirtų apskritimų centru, o reikšmės sudaro stačiakampę taškelių matricą, gaunamą keičiant polinio kampo ir spindulio reikšmes. Jei (ox,oy) pažymėti rasto rainelės centro koordinates, tai gausime tokias formules:
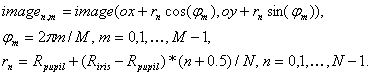
Praktiškai taikant šias formules tenka spręsti vaizdo reikšmės image(x,y) apskaičiavimo problemą, nes nuskaitytas pilkumo lygmenų rainelės vaizdas yra žinomas tik sveikaskaitėse koordinatėse, t.y. taškuose (x,y)=(i,j), kur i ir j yra sveikieji skaičiai. Mūsu atveju x = ox+r_n cos(phi_m) ir y = oy + r_m sin(phi_m) yra realūs skaičiai kurie tik retais atvejais bus sveikieji. Ši problema sprendžiama naudojant bitiesinę interpoliaciją, kurios esmė yra tokia.
- Surandami taškui (x,y) artimiausi 4-i taškai su sveikaskaitėmis koordinatėmis ( žiūr. 11 pav.). Naudojant Java programavimo operatorius (i,j) taško koordinatės bus randamos taip:
int i = (int) x;
int j = (int) y;
- Vaizdo reikšmė taške (x,y) apskaičiuojama formule
image(x,y) = image[i,j]*(1-dx)*(1-dy) + image[i+1,j]*dx*(1-dy) +
image[i,j+1]*(1-dx)*dy + image[i+1,j+1]*dx*dy.
Čia dx = x - i, dy = y j. Nesunku pastebėti, kad fiksuotam x arba y išraiška image(x,y) yra tiesinė likusio ( y arba x ) kintamojo atžvilgiu. Jei x ir y yra sveikaskaitės, t.y. x = i ir y = j, tai formule apskaičiuota reikšmė image(x,y) sutampa su vaizdo reikšme image[i,j]. Dėl šių dviejų savybių formulė ir yra vadinama bitiesine interpoliacija.
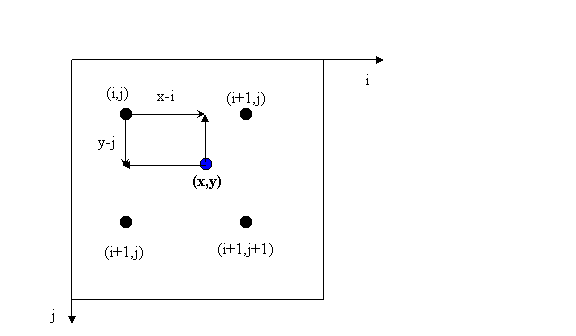
11 pav. Taško (x,y) artimiausios sveikaskaitės koordinatės naudojamos bitiesinei interpoliacijai.
Modifikuosime rainelės reikšmių apskaičiavimo išraiškas, kad jos tiktų bendru atveju kai mažojo ir didesniojo apskritimo centrai yra skirtingi. Formulių modifikacijos idėja yra gana paprasta formulėse reikia pakeisti fiksuotą centrą (ox,oy) kintamu centru (ox(r),oy(r)) taip, kad kintant spinduliui r nuo minimalios reikšmės r = R_pupil iki maksimalios R_iris centro koordinačių išraiška (ox(r),oy(r)) kistų tiesiškai nuo (ox_pupil,oy_pupil) (vyzdžio centro taškas) iki (ox_iris,oy_iris) (rainelės centro koordinatės). Atlikus šią modifikaciją gauname tokias formules:
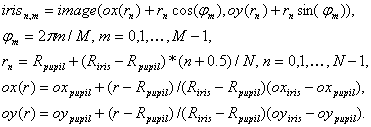
12 pav. mėlynais taškeliais pavaizduoti taškai ( x_n,m, y_n,m ), kuriuose taikant bitiesinę interpoliaciją apskaičiuojamos iris_n,m reikšmės.
12 pav. Rainelės iris_(n,m) gardelės taškai, kuriuose, taikant bitiesinę interpoliaciją, apskaičiuojamos rainelės pilkumo lygmenų reikšmės.
Sekantis paveikslėlis iliustruoja gautų bitiesine interpoliacija pilkumo lygmenų taškelių matricą. Kaip ir anksčiau, iliustracijai gauti naudojamas NIST ICE 2005 [NIST ICE 2005] rainelių duomenų bazės 242116.tiff failo rainelės vaizdas, 12 pav. atveju N = 8, M = 64, 13 pav. N = 64, M = 512, juoda 12 pav. linija žymi atkarpą ties kuria buvo perkirptas rainelės žiedas pavaizduojant jį 13 pav. pilkumo lygmenų taškeliais, apatiniai 13 pav. taškai atitinka rainelės vidinio apskritimo taškus.

13 pav. Rainelės pilkumo lygmenų 64 x 512 taškelių vaizdas.
Turint stačiakampę rainelės pilkumo lygmenų matricą galima pradėti išskyrinėti binarinius požymius. Požymiams skaičiuoti pasirenkamas koks nors filtras, juo filtruojamas rainelės vaizdas ir pagal filtravimo rezultato ženklo reikšmę priskiriama galutinė binarinio požymio reikšmė. Daugmanas filtravimui naudojo dvimatį Gaboro filtrą [Gabor filtrą]. Dvimačiai Gaboro filtrai horizontalia ir vertikalia kryptimi turi po du laisvus parametrus, kurių konkrečios reikšmės literatūroje nenurodomos, todėl praktiškai neįmanoma atkartoti autorių gaunamų rainelių atpažinimo rezultatų gaunamų taikant šį filtravimą. Todėl mes naudosime paprastesnius vienmačius filtrus ir nurodysime konkrečias filtrų koeficientų reikšmes. Kadangi binariniai požymiai gaunami remiantis filtravimo rezultato ženklu, aišku, kad filtro koeficientų suma turi būti lygi nuliui. Jei pavyzdžiui vidutinė filtro koeficientų reikšmė būtų teigiama, tai filtruojant rainelės vaizdo reikšmes gautume dominuojančią teigiamą filtravimo rezultato reikšmę, nes visos rainelės reikšmės yra neneigiamos ir kinta intervale [0,255]. Paprasčiausias vienmatis netrivialus filtras, kurio koeficientų suma lygi nuliui, yra
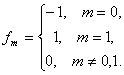
Pritaikius šitą filtrą vienmačiam signalui u_n gausime tokį filtravimo rezultatą:
![]()
kuris yra signalo u išvestinės aproksimacija. Atlikus požymio binarizaciją, pozicijoje m rašytume 1, jei u_m didesnis už u_(m-1), ir 0 priešingu atveju, kai u_m mažesnis arba lygus u_(m-1). Praktiškai įsitikinta, kad daugeliu atvejų geriau analizuoti ne funkciją arba jos išvestinę, bet jos antrosios eilės išvestinę. Antrosios eilės išvestinės skirtuminis analogas apibrėžiamas filtru
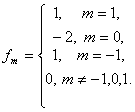
Pritaikius šį filtrą vienmačiam signalui gauname tokį rezultatą:
![]()
Šiuo atveju binarinis požymis taške m būtų apibrėžiamas išraiška
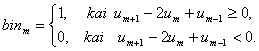
Rainelės atveju turime dvimatį signalą iris(n,m). Skaičiuoti signalo pokyčius spindulio kryptimi gana rizikinga, nes rainelės vidinis ir ypač išorinis kontūras neturi aiškiai apibrėžtos ribos. Todėl spindulio (indekso n) reikšmė r_n yra fiksuojama ir skaičiuojami pokyčiai kampo ( indekso m ) kitimo atžvilgiu. Tokiu būdu gauname binarinių požymių matricą
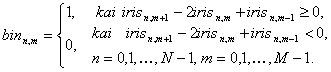
Taip skaičiuojami požymiai yra gana nestabilūs atsitiktiniam triukšmui. 14 pav. pavaizduota 32 x 256 binarinių požymių matrica bin_(n,m) apslaičiuota 242116.tiff paveiksliukui imant 32 fiksuotas r_n ( N = 32 ) ir 256 phi_m ( M = 256 ) reikšmes. Žali taškeliai žymi reikšmes bin_(n,m) = 0, o raudoni taškus bin_(n,m) = 1. Iš paveikslėlio matyti, kad dviejų autentiškų rainelių binarinių požymių matricos gali stipriai skirtis dėl smulkaus mastelio.
![]()
14 pav. 242116.tiff failo rainelės binariniai požymiai skaičiuojami pagal rainelės antrosios eilės išvestinės skirtuminio analogo skaičiuojamo kampo kryptimi.
Kad spręsti šią problemą atliksime skaičiuojamų požymių vidurkinimą spindulio ir kampo kryptimi. Paprasčiausiu atveju gaunamas vidurkinimo rezultatas bus ekvivalentus filtravimui su tokiu dvimačiu filtru:
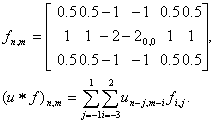
Čia 2_(0,0) žymi filtro f_(n,m) centrinį koeficientą atitinkantį indeksų reikšmes n = 0 ir m = 0. Taikant šias formules laikoma, kad u_(n-j,m-i), kai m<i arba m >= M + i, yra gaunamos periodu M pratęsiant reikšmes, t.y. u_(n-j,m-i) = u_(n-j, (M+m-i)%M). Toks periodinis pratęsimas yra natūralus, nes pradinis rainelės signalas yra periodinis kampo kryptimi. Kadangi spindulio kryptimi signalas nėra periodinis, tai pateiktose dvimačio filtravimo formulėse laikoma, kad u_(n-j,m-i) = 0, kai n<j arba n >= N + j. Atlikus minimalų vidurkinimą spindulio ir kampo kryptimis gausime 15 pav. pavaizduotą binarinių požymių matricą. Ši požymių matrica kiek panaši į 14 pav. požymių matricą tik apskaičiuotą kitu dvigubai smulkesniu masteliu.
![]()
15 pav. Binarinių požymių matrica gaunama filtruojant antrosios eilės išvestinę atitinkančiu skirtuminiu filtru vidurkintu 2 taškeliais kampo ir minimaliu trikampiu vidurkinimu spindulio kryptimi.
Daugman darbe taip pat nurodyta, kad galutinė požymių matrica formuojama naudojant kelių mastelių Gaboro filtrus. Todėl mes apibendrinsime vidurkinimo formules tuo atveju, kai imama KF vienodais svoriais vidurkinimų kampo ir (2*KR+1) trikampio lango svoriais spindulio kryptimi. Tokį vidurkinimą atitiks filtras
15 pav. atitinka vidurkinimo parametrų reikšmės KF = 2 ir KR = 1.
Rainelės šablonas
Šablonas ( angl. template ) yra formuojamas iš požymių. Šablono pradžioje gali būti antraštė ( angl. header) , kurioje įrašoma specifinė informacija, pavyzdžiui pradinio paveiksliuko katalogas ir vardas, objekto unikalus identifikatorius. Šablono antraštėje patalpinama informacija nenaudojama skaičiuojant dviejų šablonų panašumą. Likusi rainelės šablono dalis sudaroma iš binarinių požymių. Tarkime fiksuoto mastelio požymių matricai sudaryti naudosime 32 r_n ( N = 32 ) ir 256 phi_m ( M = 256 ) reikšmes, bei keturis skirtingus mastelius/vidurkinimus atitinkačius parametrus KF = 2, KR=1; KF = 3, KR = 2; KF = 4, KR = 2 ir KF = 6, KR = 3. 16 pav. iliustruoja 242116.tiff failo rainelės gaunamą šabloną. Vaizdumo dėlei 4-ių skirtingų mastelių binarinių požymių matricos atskirtos kelių taškelių baltais tarpais. Sudarant vieningą 4x32x256 bitų matricą nebūtina išdėstyti paveikslėlyje nurodyta tvarka. Pavyzdžiui gali būti patogu vieną baitą sudaryti iš dviejų ketvertukų, gaunamų sudedant greta keturių skirtingų mastelių binarinių požymių bitus. Objektus atspindintys šablonai kaip taisyklė užima žymiai mažiau vietos nei pradinė informacija. Pavyzdžiui mūsų pradinis rainelės paveikslėlis pateikiamas 640 x 480 256 pilkumo lygmenų taškeliais, kas atitnka 640 x 480 x 8 = 2457600 bitus informacijos, o tos pačios rainelės šablonas užima tik 32 x 256 x 4 = 32768 bitus, t.y. pradinė informacija suspaudžiama lygiai 75 kartus. Daugmano algoritmas naudoja dar glaudesnius šablonus, kurių dydis yra 2048 bitai binarinių požymių plius tokio paties dydžio kaukės ( angl. mask ), t.y. vieno rainelės šablono dydis yra tik 4096 bitai.
![]()
![]()
![]()
![]()
16 pav. Rainelės šablonas sudarytas iš 4 ių mastelių 32x256 binarinių požymių matricų.
Šablonų palyginimas
Beliko išsiaiškinti paskutinį rainelių atpažinimo/verifikacijos etapą, t.y. šablonų palyginimą. Verifikacijos atveju atpažinimui pateikiami du rainelių šablonai ir reikia priimti sprendimą ar tie šablonai atitinka vieną ir tą pačią rainelę ar tai yra šablonai gauti iš skirtingų rainelių. Kaip taisyklė pirmasis šablonas yra išsirenkamas iš iš anksto įrašytos rainelių duomenų bazės pagal asmens prisistatymą, pvz. klaviatūroje surinktą vardą/pavardę ar kokį nors asmenį identifikuojantį kodą, o antrasis šablonas sudaromas operatyviai nuskenavus asmens rainelę ir atlikus pilną rainelės lokalizavimo bei požymių išskyrimo procedūrą. Taigi verifikacijos metu reikia įvertinti dviejų šablonų panašumą. Šablonų panašumas įvertinamas lyginant atskirus šablonų bitus. Jei dviejų šablonų atitinkamose pozicijose bitai sutampa (t.y. 0 = 0 arba 1 = 1 ), tai panašumo metrika padidinama vienetu. Paprastumo dėlei laikysime, kad šablone yra įrašyta K x N x M =L bitų bin_l, l = 0, 1, ..., L-1, kur K yra mastelių skaičius, N skirtingų spindulių skaičius, M kampų skaičius[1]. Tuomet dviejų šablonų panašumas ( angl. similarity ) gali būti įvertintas taip
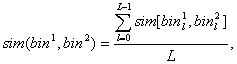
kur sim[a,b] = 1, kai a = b ir sim[a,b] = 0, kai a != b. Kitaip tariant panašumas yra dviejuose šablonuose sutapusių bitų dalis. Deja tokia paprasta panašumo samprata duoda nelabai aukštą rainelių verifikacijos kokybę. Taip atsitinka dėl to, kad dvi skirtingos tos pačios rainelės nuotraukos gali būti kiek pasisukusios kampu phi0 ir prielaida, kad abiejų rainelių kampų reikšmės vieningoje koordinačių sistemoje sutampa, t.y. phi^1_m = phi^2_m, yra neteisinga ir turėtų būti patikslinta pvz. phi^1_m = phi^2_m + phi0 formule. Tačiau praktiškai posūkio phi0 reikšmė būna nežinoma, tuo labiau, kad bendru atveju dėl rainelių nestandžių deformacijų ir lokalizacijos paklaidų kiekvienam m gali būti kiek kita posūkio phi0 reikšmė. Todėl praktiškai yra fiksuojamas ieškomo posūkio phi0 tikslumas deltaRot, pasirenkamas galimų posūkių skaičius NRot ( pvz. Daugman naudoja NRot = 3 ) ir ieškomas maksimalus panašumas
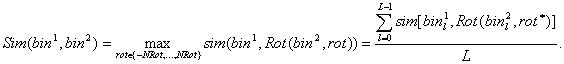
Kaip taisyklė Rot(bin_l,rot) = bin_(l+rot), tačiau jei (l+rot>=L) arba l ir ( l+rot) yra skirtingų spindulių eilutėse, indeksas (l+rot) paslenkamas kartotiniu eilutės periodu M taip, kad l ir ( l+rot+mM) būtų vienoje eilutėje. Pavyzdžiui, jei M = 256 ir formuojant šabloną naudojama 16 pav. iliustruojama skirtingų mastelių išdėtymo tvarka, tai
Rot(bin^2_254,7) = bin^2_5.
Kad palyginti skirtingų panašumo metrikų kokybę ir parinkti optimalius požymių išskyrimo ir palyginimo algoritmų parametrus naudosime JAV nacionalinio standartizacijos instituto ICE 2005 rainelių duomenų bazę [ NIST ICE 2005 ]. Rainelės lokalizavimo mes neoptimizuosime, taip pat fiksuosime 4 požymių mastelius, spindulių skaičių N = 32 ir kampų M = 256. 17 pav. iliustruoja dviejų skirtingų rainelių palyginimo algoritmų kokybę. Mėlyna spalva pažymėta verifikacijos kokybės kreivė ROC [ROC] gaunama tiesiogiai lyginant du šablonus, t.y. atveju NRot = 0, o kita, žaliai nuspalvinta kreivė, gauta atveju NRot = 4, kas atitinka 1 + 2 * 4 = 9 skirtingus rainelės poslinkius (postūmius šablonų atveju). Kadangi žalia ROC kreivė visuose taškuose žemiau mėlynos ROC kreivės, tai vienareikšmiai galime teigti, kad šių duomenų bazei antrasis šablonų palyginimo variantas tinka geriau. Atkreipkite dėmesį, kad skaičiuojant ROC kreivę panašumo įverčiai buvo skaičiuojami ne visose galimose apsišaukėlių porose. Taip daroma gana dažnai, nes didelių duomenų bazių atveju galima sudaryti labai daug apsišaukėlių porų ir taupant skaičiavimo laiką galima skaičiuoti panašumo įverčius ne visoms, o pavyzdžiui tik kas 16 ar 64 apsišaukėlių porai. Autentiškų porų palyginus būna mažiau, todėl nesunku joms visoms apskaičiuoti panašumo įverčius.
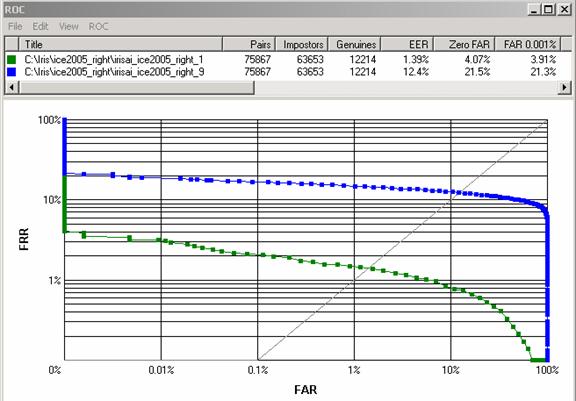
17 pav. NIST ICE 2005 Right Iris duomenų ROC kreivės gaunamos naudojant nesukiojamus šablonus (mėlyna kreivė ) ir sukiojamus 9 pozicijose ( žalia kreivė ).
Pasiūlysime dar keletą šablonų palyginimo modifikacijų, kurios gerina verifikacijos kokybę. Lyginamų šablonų poslinkius galima atlikti ne tik kampo kryptimi bet ir spindulio kryptimi. Idealaus rainelių lokalizacijos atveju tokie poslinkiai neturi prasmės, tačiau nedideles vyzdį ir rainelę ribojančių apskritimų spindulių suradimo paklaidas galima ištaisyti šablonų palyginimo metu slenkant šablonus keliais taškeliais spindulio kryptimi. Turint K mastelių ir M vieno mastelio skirtingų kampų atliekant vieno taškelio poslinkį spindulio kryptimi reikia bin_l reikšmę pakeisti bin_(l + K*M) reikšme. Gana kebli problema yra lyginti nestandžiai deformuotas raineles. Nedaug pakėlus/nuleidus, pasukus/pakreipus galvą tos pačios akies skenuotas rainelės vaizdas išsitampo ir dviejų apskritimų modelis nepilnai sugeba kompensuoti atsiradusius iškraipymus. Šiai problemai spręsti siūlome suskaidyti rainelės gardelės taškus atskirais sektoriais. 18 pav. pavaizduotas gardelės taškų grupavimas 8 sektoriais. Laikysime, kad vieno sektoriaus ribose deformacijos yra pakankamai mažos ir lygindami dviejų rainelių požymius ieškosime šablonų optimalių poslinkių kampo ir spindulio kryptimis.
|
7 q ą 6 q ą 4 q ą 3 q ą 2 q ą 1 q ą 0
![]()


![]()
![]()
![]()
![]()
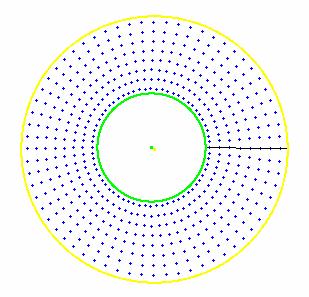
18 pav. Rainelės gardelės taškų suskaidymas į 8 sektorius.
Tarkime KRot yra teigiamų poslinkių skaičius kampo kryptimi, o KShift teigiamų poslinkių skaičius spindulio kryptimi. Atliekant poslinkį spindulio kryptimi susiduriame su krašto problema, nes šiuo atveju periodinis reikšmių pratęsimas būtų nelogiškas. Sprendžiant šią problemą galima apsiriboti mažesniu lyginamų taškelių skaičiumi, pavyzdžiui KMx(N-2KShift) parenkant juos taip, kad visi teigiami ir neigiami poslinkiai tilptų KMxN binarinių požymių matricoje. Kitas sprendimas taškeliams, kurių indeksai išeina iš KMxN matricos ribų priskirti su tikimybe 0.5 reikšmę 0 arba 1 ir lyginti pilnas KMxN taškelių matricas. Kadangi pagal filtravimo ženklą parenkamų binarinių požymių reikšmės gana tiksliai su vienoda tikimybe 0.5 yra lygios 0 arba 1, tai toks santykinai nedidelio iš ribų išeinančių taškelių pakeitimas atsitiktiniais 0 arba 1 nežymiai keičia palyginimo rezultatą ir sprendžia gana sudėtingą problemą kokį atlikti normavimą lyginant skirtingų dydžių binarinių požymių matricas.
Tarkime suskaidėme gardelę į S sektorių. Tokiu atveju maksimizuodami atžvilgiu KShift ir KRot poslinkių kiekvieno lyginamo sektoriaus binarinių požymių sutapimo procentą turėsime
![]()
laisvės laipsnių. Didėjant S šis skaičius greitai auga ir todėl apsišaukėlių poros gali atsitiktinai įgyti dideles panašumo reikšmes. Šiai problemai spręsti siūlome tokią dinaminiu programavimu paremtą procedūrą:
int[][] score = new int[2*KShift+1][2*KRot+1];
for ( sector = 0; sector < S; s++)
for ( k = -KShift; k <=KShift;ki++)
for ( r = -KRot; r<= KRot; r++)
score[k+KShift][r+ KRot] +=
similarity(shift(bin1,k),rot(bin2))
+ max( score[k+KShift][r+KRot],
score[k-1+KShift][r+ KRot],
score[k+1+KShift][r+ KRot],
score[k+KShift][r-1+ KRot],
score[k+KShift][r+1+ KRot]);
Realizuojant max(score ...) skaičiavimą reikia pasirūpinti, kad indeksų ribos neišeitų iš rėžių, pvz. score[k-1+KShift][r+KRot] pakeisti score[max(0,k-1+KShift)][r+KRot]. Dviejų šablonų panašumo reikšmė įvertinama dvimačio score masyvo maksimumu. Taip skaičiuojamas panašumas mažų autentiškų rainelių deformacijų atveju surinks didelį panašumo taškų skaičių, o apsišaukėlių atveju panašumo reikšmė turi mažiau šansų surinkti daug panašumo taškų, nes dabar laisvės laipsnių skaičius mažesnis nei
![]() .
.
19 pav. iliustruoja verifikacijos ROC kreivės pagerėjimą gautą aprašytu algoritmu, kurio parametrai yra S = 16, N = 32, M = 256, KShift = 2, KRot = 4.
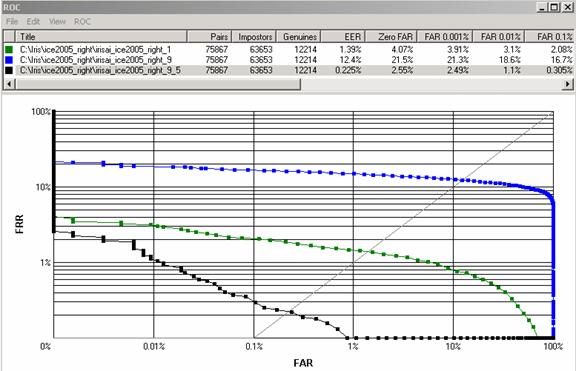
19 pav. 17 pav. ROC kreivės papildytos juoda verifikacijos ROC kreive, kuri gauta palyginimo algoritmu naudojančiu 16 sektorių, 9 poslinkius kampo kryptimi, 5 poslinkius sindulio kryptimi ir dinaminio programavimo panašumo taškų skaičiavimo algoritmą.
Praktinė užduotis.
Realizuokite aprašytą rainelių požymių apskaičiavimo, šablonų sukūrimo ir jų palyginimo algoritmą. Planuojama užduoties trukmė 4 savaitės.
1 sav. Kokio nors rainelės vaizdo, patalpinto http://uosis.mif.vu.lt/atpazinimas/iris/ice2005/Spring2004iris/
adresu, duomenų nuskaitymas ir pavaizdavimas kompiuterio ekrane (0.2 balo)
Naudojantis http://uosis.mif.vu.lt/atpazinimas/iris/ice2005/irisai_ice2005_left.info
faile pateikta informacija nuskaityti rainelės lokalizacijos duomenis įrašytus
ox_pupil oy_pupil radius_pupil ox_iris oy_iris radius_iris
tvarka ir pavaizduoti 10 pav. analogą, turint omenyje, kad informacija apie 242116.tiff failo rainelės apskritimus įrašyta 434 http://uosis.mif.vu.lt/atpazinimas/iris/ice2005/irisai_ice2005_left.info failo eilutėje (0.3 balo).
2 sav. Nuskaityti tekstinį *.bxml
http://uosis.mif.vu.lt/atpazinimas/iris/ice2005/ICE_Exp_1.0.1_Target_Templates.bxml
failą (0.1 balo)
Suformuoti NIST ICE 2005 rainelių sąrašą, remiantis http://uosis.mif.vu.lt/atpazinimas/iris/ice2005/ICE_Exp_1.0.1_Target_Templates.bxml
faile pateikta informacija. Tiff formato failų vardai nurodomi lauke
complex-presentation
o identifikatoriai lauke
complex-biometric-signature.
Pavyzdžiui informaciją apie 242116.tiff failą yra kito failo
http://uosis.mif.vu.lt/atpazinimas/iris/ice2005/ICE_Exp_1.0.2_Target_Templates.bxml
eilutėse
<complex-presentation name="242116" modality="IRIS" >
<complex-biometric-signature name="291025" quality="5">
Teisingai nuskaičius duomenis turite gauti 1425 rainelių tiff failų vardus ir jų identifikatorius. ( 0.4 balo)
3 sav. Realizuoti bitiesinės interpoliacijos formulę suformuojant 13 pav. parodytą vaizdą (0.2 balo).
Suformuoti 1425 rainelių NIST ICE 2005 right šablonų bazę įrašant duomenis į vieną failą (0.3 balo).
4 sav. Realizuokite rainelių šablonų palyginimo algoritmą, kuriame neatliekami posūkiai ir suformuokite *.roc formato failą, kad būtų galima pažiūrėti ROC kreivę (0.2 balo).
Realizuokite šablonų palyginimo variantą, kuris naudoja posūkius. Pavaizduokite gautų NIST ICE 2005 right šablonų bazės verifikacijos ROC kreivę (0.3 balo).
Kitas keturias savaites galite tobulinti savo algoritmą. Pagal pasiektus rezultatus bus skiriami priziniai balai už ROC kreivės kokybę ( iki 5 ezgamino balų ). Kad suvienodinti sąlygas, naudojami verifikacijai šablonai turi būti vienodo dydžio: 48 + 2x4096 = 8240 baitų. Pirmieji 48 baitai skiriami nestandartizuotai antraštei, sekantys 4096 binarinių požymių matricai, likę 4096 kaukei arba papildomiems binariniams požymiams, jei kaukės nenaudojate. Topinis 4096 baitų išskaidymas gali būti toks:
4x256x32 bitų =4096 baitų ( 4 - masteliai, 256 rainelės taškelių skaičius horizontalia kryptimi, 32 vertikalia.
Literatūra
[Daugman, 1993] Daugman, J. (1993) "High confidence visual recognition of persons by a test of statistical independence." IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 15(11), pp. 1148-1161.
Skenuotą straipsnio kopiją autorius patalpino http://www.cl.cam.ac.uk/~jgd1000/PAMI93.pdf adresu.
[Iridian Technologies] Iridian Technologies kompanijos tinklalapis http://www.iridiantech.com/
[Wikipedia, Iris recognition] Iris recognition, http://en.wikipedia.org/wiki/Iris_recognition.
[Daugman techreport 635] John Daugman, Results from 200 billion iris cross-comparisons, http://www.cl.cam.ac.uk/techreports/UCAM-CL-TR-635.pdf
[ICAO] International Civil Aviation Organization, http://www.icao.int/
[Schiphol] Amsterdam Schiphol Airport, http://en.wikipedia.org/wiki/Schiphol_Airport
[UAE] United Arab Emirates, http://en.wikipedia.org/wiki/United_Arab_Emirates
[UK IRIS] IRIS - Iris recognition immigration system, http://www.ind.homeoffice.gov.uk/applying/iris/
[NIST ICE 2005 ] Iris challenge evaluation, http://iris.nist.gov/ice/
[Interlacing] Interlacing, http://neuron2.net/LVG/interlacing.html
[Integral Image] Feature detection using Integral Image, http://www.ais.fraunhofer.de/~surmann/papers/icra2005/node12.html
[Bilinear Interpolation] Bilinear Interpolation, http://en.wikipedia.org/wiki/Bilinear_interpolation
[Circular Hough Transform] Circular Hough Transform, http://ipml.ee.duth.gr/~papamark/GHT/Help/CHT.htm
[Gabor Filter] Gabor filter,
http://en.wikipedia.org/wiki/Gabor_filter
[ ROC ] Atpažinimo sistemos kokybės įvertinimas ir jo vizualizacija ( ROC kreivė ),
http://uosis.mif.vu.lt/~bastys/academic/ATE/ROC/ROC.htm