
Kas yra minimalus žiedas?


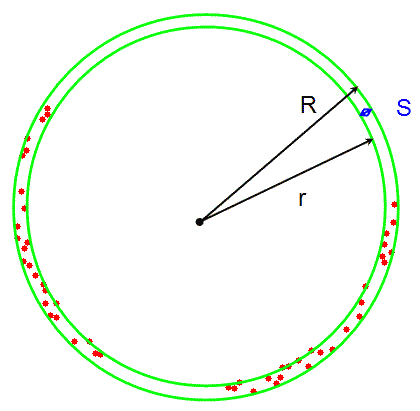
1-2 paveikslėlis. Plokštumos taškų aibė ir jos minimalus žiedas
Plokštumos taškų Mi, i=0,...,N-1, minimaliu žiedu vadiname minimalaus storio S žiedą į kurį patenka visi duotieji taškai Mi.
Angliškas minimalaus žiedo terminas yra minimum-width annuli. Literatūrą internete galite rasti pagal šiuos raktinius paieškos žodžius arba paskaityti kokį nors kompiuterinės geometrijos vadovėlį [1].
1 paveikslėlyje pavaizduota 49 plokštumos taškų aibė, kuriai reikia rasti minimalų žiedą. 2 paveikslėlis iliustruoja šios uždavinio sprendimą.
Norint gauti minimalų žiedą reikia rasti:
kad žiedo storis S=R-r būtų minimalus.
Fiksavus bet kokį centro tašką O galima rasti minimaliai ir maksimaliai nutolusį nuo O tašką Mi. Mažiausias atstumas sutaps su r, o didžiausias su R. Taigi r visuomet yra nedidesnis už R.
Taikymai
Minimalus žiedas gali būti taikomas:
Išspręskime tokį fizikos uždavinį.
Tarkime erdvėje duota aibė žvaigždžių, kurios vienu metu virsta supernovomis. Kokiame erdvės taške reikia patalpinti stebėtoją, kad stebėjimo laikotarpis nuo pirmosios stebimos supernovos iki paskutinės užtruktų kuo trumpiau.
Šio fizikinio uždavinio plokščiasis analogas ekvivalentus minimalaus žiedo suradimui.
Pramonėje susiduriama su minimalaus žiedo problema įvertinant gaminio apvalumą. Tarkime svarbu, kad guoliai būtų idealiai apskriti. Išmatavus su lazeriu atstumą iki įvairių guoliaus paviršiaus taškų, jo apvalumo kokybę galima įvertinti sprendžiant minimalaus storio žiedo paieškos uždavinį.
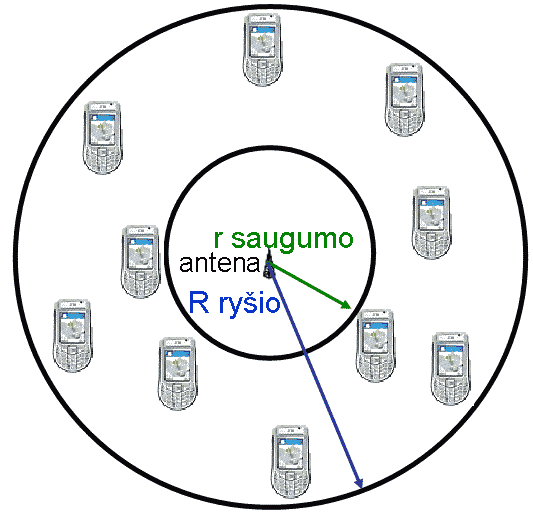
Tarkime projektuotojui reikia parinkti optimalią vietą mobiliųjų telefonų signalų retransliacijos antenai taip kad būtų tenkinami klientų saugumo pageidavimai (maksimizuojamas atstumas nuo antenos) ir pasiekiamas geras ryšys (minimizuojamas maksimalus atstumas iki vartotojo). Jei klientų namų koordinatės yra žinomos, šį projektavimo uždavinį galima spręsti panaudojant minimalaus žiedo paieškos algoritmą.
Mūsų kurso atžvilgiu aktualiausias yra trečiasis punktas, kurį atskleisime kiek plačiau.
Kaip minimalus žiedas gali praversti atpažinime?
Kadangi geometriškai akivaizdu, kad minimalus žiedas yra viena galimų duomenų (plokštumos taškų) aproksimacijos formų, tai tuo pačiu ši konstrukcija naudinga ir atpažinimui. Reikalas tame, kad kompresijos ir atpažinimo uždaviniai yra giminingi. Tarkime žiūrint į skaičių paveikslėlį jūs jame išskiriate atskiras dalis, kurias identifikuojame skaitmenimis (nuo 0 iki 9).
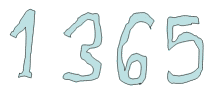
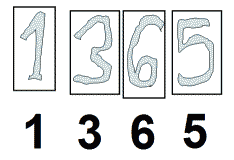
3-4 paveikslėlis. Skaičiaus "vaizdelis" ir jo atpažinimo/kompresijos schema.
Taigi atpažinimas ekvivalentus aukščiausio laipsnio kompresijai, kurio dėka skaičiaus paveikslėlis virsta kelių skaitmenų informacija. Realūs vaizdai dažnai atpažįstami pagal kontūrą, kurį galima gabalais aproksimuoti tiesės atkarpomis arba apskritimo lankais. Tokia aproksimacija koncentruoja informaciją į apskritimų lankus aprašančius parametrus (centrus, spindulius, lanko pradžia/pabaiga), kuriuos galima efektyviai naudoti atpažinimui.



5-6-7 paveikslėlis. Piršto pradinis vaizdas , "Meksikietiška skrybėle" filtruotas pirštas, ekstremalių taškų kontūrai
Paimkime piršto atspaudo vaizdą (paveikslėlis 5). Kad būtų lengviau vaizde išskirti kontūrus, pritaikykime pradiniam vaizdui "Meksikietiškos skrybėlės" filtrą. Filtravimo operacija fiksuotam vaizdo taškui daugina aplinkinius vaizdo taškelius iš filtru apibrėžiamų konstantų ir grąžina sandaugų algebrinę sumą. Analogiška filtravimo operacija atliekama slenkančiu langu imant vis naujus centrinius ir jų aplinkinius taškelius ir taip gaunama filtruotų reikšmių matrica, vadinama filtruotu vaizdu. "Meksikietiškos skrybėlės" filtro visų koeficientų suma lygi nuliui, artimi centrui filtro koeficientai yra teigiami, tolimesni - neigiami, filtro koeficientų reikšmės priklauso tik nuo indeksų taško atstumo iki centrinio indekso taško. Vaizduojant trimatį tokio filtro grafiką gaunamas panašus į "Meksikietiškos skrybėlės" vaizdą. Iš čia ir kilo filtro pavadinimas. 6 paveikslėlis iliustruoja po filtravimo gaunamą rezultatą. Grupuojant teigiamus ir neigiamus filtruoto vaizdo ekstremumų taškus gauname kreives, kurias natūralu aproksimuoti apskritimų lankais.



8-9-10 paveikslėlis. To paties piršto atspaudo kitas pradinis vaizdas, "Meksikietiška skrybėle" filtruotas piršto atspaudas, ekstremalių taškų kontūrai
8-9-10 paveikslėliai iliustruoja analogiškus to paties piršto atspaudo vaizdus. Nors pirštas yra tas pats, tačiau vaizdai vienas kito atžvilgiu yra pasukti, paslinkti, prispaustos dalinai skirtingos pirštų atspaudų dalys. Atpažinimo prasme susiduriame su klasikine problema: reikia sukurti algoritmą, kad su kompiuterio pagalba surastume apytiksliai posūkio kampą bei poslinkio parametrus, kad vėliau atlikti vaizdų panašumo tikrinimą. Jei neaptiksime arba rasime su didelėmis klaidomis posūkio ir poslinkio parametrus, tai pradinių vaizdų palyginimas kaip taisyklė duos dideles reikšmes ir būsime priversti paskelbti, kad vaizdai yra skirtingų asmenų pirštų arba kitaip tariant pirštų atspaudus su kompiuteriu atpažinsime neteisingai.
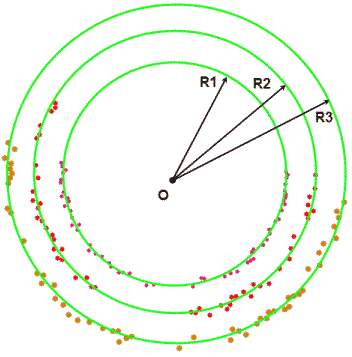
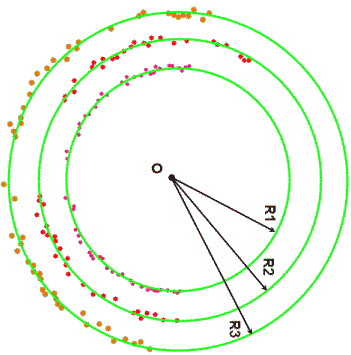
11-12 paveikslėlis. Trijų taškų grupių aproksimavimas apskritimais ir pasuktų bei paslinktų tų pačių taškų grupių aproksimavimo žiedais parametrai.
Iš 11-12 paveikslėlių matyti, kad aproksimavimo apskritimais parametrai R1, R3 ir R3 yra invariantiški posūkio bei poslinkio grupėms. Dėl šios puikios savybės ir yra tikslinga kontūrus vaizduose aproksimuoti apskritimais. Aproksimuojantį apskritimą natūralu apibrėžti minimalaus žiedo viduriu einančiu apskritimu, nes tokiu atveju aproksimuojami taškai bus arčiausiai tokio apskritimo.
Algoritmai
Kyla klausimas ar bet kokiai plokštumos taškų aibei galima rasti jos minimalų žiedą. Kadangi aproksimuojamų žiedų taškų skaičius yra baigtinis, tai fiksavus bet kokį centro tašką O rasime minimaliai ir maksimaliai nuo centro taško O nutolusius taškus. Apskaičiavę maksimalaus ir minimalaus atstumų skirtumus gausime taškus Mi aproksimuojančio žiedo su centru taške O storį. Akivaizdu, kad žiedo storis tolydžiai priklauso nuo jo centro O padėties. Apibrėžkime apie taškus minimalaus spindulio apskritimą. Kai centro taškas O artėja į begalybę, aproksimuojančio žiedo storis neviršys apibrėžto apie taškus apskritimo spindulio. Kita vertus bet kokio aproksimuojančio žiedo storis bus neneigiamas. Tuo atveju, kai per visus duotuosius taškus galima nubrėžti apskritimą, tai jis ir bus minimalus nulinio storio žiedas. Šie tolydumo ir žiedo storio aprėžtumo samprotavimai įrodo minimalaus žiedo egzistavimą.
Pasiūlysime keletą minimalaus žiedo suradimo algoritmų. Kuriant algoritmus mums bus naudinga tokia teorema.
Teorema. Tarkime yra duota N≥4
skirtingų plokštumos taškų M0, M1, ..., MN-1,
kuriems reikia rasti minimalų žiedą. Tuomet tarp šių taškų
atsiras keturi taškai A=Mi1, B=Mi2, C=Mi3,
D=Mi4, iš kurių pirmieji du (A ir B) priklausys vidiniam apskritimo
minimaliam žiedui, o likę du (C ir D) priklausys išoriniam minimaliam žiedui.
Minimalaus žiedo centras bus statmenų išvestų per atkarpų [A,B] ir [C,D]
vidurio taškus susikirtimo taškas.
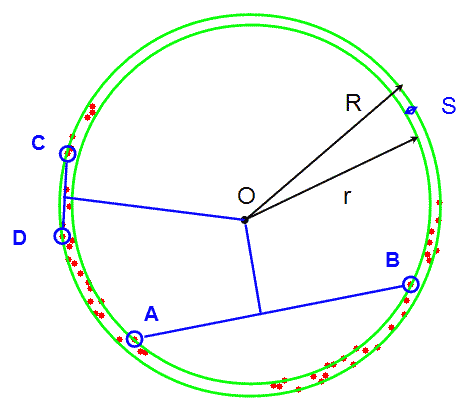
13 paveikslėlis. Minimalus žiedas ir aproksimuojami taškai priklausantys žiedo vidiniam (A ir B) ir išoriniu apskritimui (C ir D).
13 paveikslėlis iliustruoja teoremos teiginį. Mėlynai išskirti taškai A ir B priklauso vidiniam minimalaus žiedo apskritimui, o C id D - išoriniam. Per [A,B] ir [C,D] atkarpų vidurio taškus išvesti statmenys kertasi taške O, kuris yra minimalaus žiedo centro taškas.
Ši teorema šiek tiek gimininga gerai žinomam euklidinės geometrijos teiginiui, kad per bet kurio trikampio viršūnes galima nubrėžti apskritimą ir šio apskritimo centras yra statmenų einančių per trikampio karštinių vidurio taškus susikirtimo taškas. Teoremos įrodymas remiasi samprotavimu, kad bent po vieną tašką priklausys vidiniam ir išoriniam žiedo apskritimui. Jei priklausytų tik po vieną tašką, tai galėtume kiek pakeisti žiedo centro tašką taip kad išoriniam ir vidiniam apskritimui priklausytų ir patys taškai ir kad naujo žiedo storis būt kiek mažesnis. Vadinasi prielaida kad minimalaus žiedo vidiniam ir išoriniam apskritimui priklauso tik po vieną aproksimuojamą tašką yra neteisinga. panašiai samprotaudami rasime kad tik trys taškai taip pat negali priklausyti minimalaus žiedo vidiniam ir išoriniam apskritimui nes ir šiuo atveju galėsime keisti tiesėje einančioje per žiedo centrą naujų žiedų padėtį ir galėsime atrasti naują mažesnio storio žiedą. Tai ir įrodo teoremą.
Panaudodami suformuluotą teoremą gausime tokį tiesioginį taškų M0, M1, ..., MN-1 minimalaus žiedo paieškos algoritmą.
for (int i=0; i<N-3; i++) for (int j=i+1; j<N-2; j++) for (int k=0; k<N-1; k++){ for (int l=k+1; l<N; ++){ // Surandame statmenų išvestų per atkarpų // [Mi,Mj] ir [Mk,Ml] // vidurio taškus susikirtimo tašką O // ir surandame atstumus // r=min{|OMi|,|OMk|} // R=max{|OMi|,|OMk|} ... for (int n=0; n<N; ++) // Tikrinti ar taško Mn atstumas iki centro taško O // yra nemažesnis už r ir nedidesnis už R. ... // Jei visi Mn taškai tenkina šias sąlygas, // tai papildome galimų minimalaus žiedo kandidatų aibę centro tašku O ... } } } // Tarp visų galimų minimalaus žiedo centrų išrenkame tą centrą, kurio // atitinkamų R ir r skirtumas yra mažiausias.
Suformuluota teorema garantuoja, kad bent vienas taškų ketvertas atsiras. Kadangi tikrinamų sąlygų skaičius yra baigtinis, per baigtinį laiką rasime minimalų žiedą.
Šio tiesioginio minimalaus žiedo paieškos algoritmo sudėtingumas yra O(N5). Pastebėkime, kad tai yra polinominio sudėtingumo algoritmas ir sudėtingumo laipsnis yra eile didesnis už analogišką tiesioginį Delaunė trianguliacijos paieškos algoritmą.
Pasiūlysime keletą idėjų, kurios sumažins minimalaus žiedo paieškos sudėtingumo laipsnį.
Paskutinį algoritmo žingsnį, t.y. tikrinimą ar fiksuotiems keturiems taškams rastas žiedo centras pasižymi savybe, kad į jį patenka visi duotieji taškai Mn galima išspręsti efektyviau. Tuo tikslu prieš vykdant tiesioginį algoritmą reikėtų atliktą tokius parengiamuosius skaičiavimus.
for (int i=0; i<N-1; i++){ for (int j=i+1; j<N; j++){ for (int k=0; k<N; k++){ // Surandame apskritimo kertančio taškus // Mi,Mj ir Mk // spindulį Ri,j,k ... } // Fiksuotiems i ir j tarp visų Ri,j,k surandame mažiausiąjį ir didžiausiąjį: // ri,j=min{k=0,1,...,N-1}Ri,j,k, // Ri,j=max{k=0,1,...,N-1}Ri,j,k, } }
Rasti ri,j ir Ri,j tiesioginiame algoritme leis atsisakyti penktojo ciklo pagal n, nes naudojant ri,j ir Ri,j bus galima nustatyti ar i,j,k,l indeksais apibrėžtas žiedas tenkiną sąlygą kad visi Mn taškai yra žiedo viduje.
ri,j ir Ri,j reikšmių radimo sudėtingumas yra O(N3). Todėl algoritmo bendras sudėtingumas bus tik O(N4).
Nesunku algoritmo sudėtingumą supaprastinti dar viena eile. Pastebėkime, kad minimalaus žiedo išorinio apskritimo viduje yra visi plokštumos taškai Mn. Todėl išoriniam apskritimui priklausantys du taškai būtinai priklausys taškų tiesinio apvalkalo kraštui. Vadinasi pirma galime rasti tiesinį apvalkalą ir naudoti jo kraštinius taškus minimalaus žiedo paieškoje. Pateiksime supaprastinto algoritmo schemą.
for (int i=0; i<N-1; i++) Jei Mi yra tiesinio apvalkalo kraštinis{ for (int j=i+1; j<N; j++) Jei Mi yra tiesinio apvalkalo kraštinis{ for (int k=0; k<N-1; k++){ for (int l=k+1; l<N; ++){ // Naudodami ri,j ir Ri,j // patikriname ar visi Mn taškai // yra taškų Mi,Mj ir MkM,l // apibrėžto žiedo viduje ... // Jei visi Mn taškai tenkina šias sąlygas, // tai papildome galimų minimalaus žiedo kandidatų aibę centro tašku O ... } } } } // Tarp visų galimų minimalaus žiedo centrų išrenkame tą centrą, kurio // atitinkamų R ir r skirtumas yra mažiausias.
Koks yra naujo algoritmo sudėtingumas. Tipiniu atveju tik O(N1/2) taškų priklausys tiesinio apvalkalo kraštui. Todėl tokiu atveju algoritmo sudėtingumas bus O(N2/2+2)=O(N3).
Ar galima sumažinti algoritmo sudėtingumą dar? Naujame algoritme dėl ciklų pagal k it l atsiranda O(N2) sudėtingumo daugiklis. Šį daugiklį galima sumažinti iki O(N). Tuo tikslu pastebėkime, kad minimalaus žiedo viduje nėra nei vieno Mn taško. Vidinį apskritimą galima didinti taip kad jis vis viena eitų per tuos pačius du taškus tol, kol pasieksime trečiąjį tašką Mn. Toks apskritimas eis per tris taškus Mi ir jo viduje nebus nei vieno taško Mn. Vadinasi šis trejetas tenkina Delaunė trianguliacijos principą.
Remiantis šiais pastebėjimais galime patikslinti pradinę teoremą.
Teorema (patikslinta). Tarkime yra duota N≥4
plokštumos taškų M0, M1, ..., MN-1,
kuriems reikia rasti minimalų žiedą. Tuomet tarp šių taškų
atsiras keturi taškai A=Mi1, B=Mi2, C=Mi3,
D=Mi4, iš kurių pirmieji du (A ir B) priklausys vidiniam apskritimo
minimaliam žiedui, o likę du (C ir D) priklausys išoriniam minimaliam žiedui.
Taškai A ir B yra kurio nors Delaunė trianguliacijos
trikampio viršūnės, o C ir D yra taškų Mn tiesinio
apvalkalo krašte.
Minimalaus žiedo centras bus statmenų išvestų per atkarpų [A,B] ir [C,D]
vidurio taškus susikirtimo taškas.
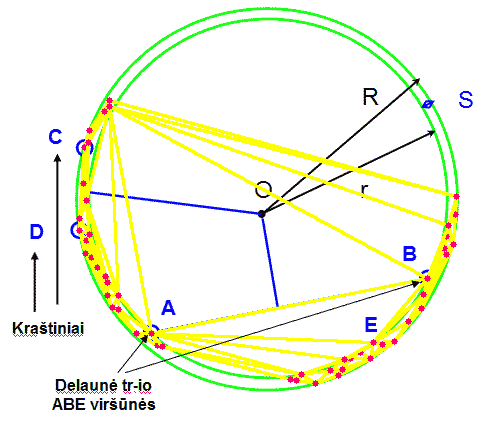
14 paveikslėlis. Minimalus žiedas ir aproksimuojami taškai priklausantys žiedo vidiniam (A ir B) ir išoriniu apskritimui (C ir D). Taškai A ir B yra vieno (ABE) Delaunė trianguliacijos trikampio viršūnės, o C ir D yra duotųjų taškų tiesinio apvalkalo kraštiniai taškai.
14 paveikslėlis iliustruoja patikslintos teoremos teiginį.
Patikslinta teorema pagrindžia tokį minimalaus žiedo paieškos algoritmą.
// Surandame duotųjų taškų Mn tiesinį apvalkalą // Tai galima atlikti panaudojant O(N log N) veiksmų ... // Surandame Mn taškų Delaunė trianguliaciją. // Tai taip pat galima atlikti panaudojant O(N log N) veiksmų ... for (int i=0; i<N-1; i++) Jei Mi yra tiesinio apvalkalo kraštinis{ for (int j=i+1; j<N; j++) Jei Mi yra tiesinio apvalkalo kraštinis{ for (int k,l=0; k,l<N; k,l++) Jei [Mk,Ml] yra Delaunė trianguliacijos kurio nors trikampio kraštinė { // Naudodami ri,j ir Ri,j // patikriname ar visi Mn taškai // yra taškų Mi,Mj ir MkM,l // apibrėžto žiedo viduje ... // Jei visi Mn taškai tenkina šias sąlygas, // tai papildome galimų minimalaus žiedo kandidatų aibę centro tašku O ... } } } // Tarp visų galimų minimalaus žiedo centrų išrenkame tą centrą, kurio // atitinkamų R ir r skirtumas yra mažiausias.
Kadangi Delaunė trianguliacijos trikampių skaičius yra O(N), tai tipiniu atveju minimalaus žiedo paieškos sudėtingumas tampa O(N2). Netipinių duomenų pavyzdžiu galėtų būti atvejis, kai visi duotieji taškai priklauso vienam apskritimui arba yra artimi tokiam atvejui. Tuomet tiesioginis aprašyto algoritmo taikymas būtų neefektyvus ir reikalautų iki O(N3) veiksmų.
http://citeseer.ist.psu.edu/agarwal99approximation.html aprašytas atrodo šiai dienai pats efektyviausias minimalaus žiedo paieškos algoritmas. Jo sudėtingumas yra O(N3/2+eps).
Praktinis darbas
Realizuokite kokį nors minimalaus žiedo paieškos algoritmą Java kalba.
Jūsų algoritmas bus vertinamas
pagal atlikimo greitį dideliems N.
Duomenis testavimui generuokite tokiu metodu:
public static List randomZiedas(int N,double d){
List L=new Vector();
int[] ri=my.randperm(N,null), fi=my.randperm(N,ri);
Random rnd=new Random(N+((long)N)<<31);
int N2=N/2, o=8*N, R=o, r=(int)(R*(1-d));
double hr=(R-r)/(double)N, f0=(rnd.nextDouble()+2)*Math.PI/4, hf=Math.PI/N/2;
for (int i=0; i<N; i++)
if (fi[i]<N2)
L.add(new Point(o+(int)((r+ri[i]*hr)*Math.cos(i*hf)),
o+(int)((r+ri[i]*hr)*Math.sin(i*hf)),i));
else L.add(new Point(o+(int)((r+ri[i]*hr)*Math.cos(f0+i*hf)),
o+(int)((r+ri[i]*hr)*Math.sin(f0+i*hf)),i));
return (List)L;
}
Metodo parametras N apibrėžia plokštumos taškų skaičių, o d - žiedo skersmens ir spindulio santykį.
Tiesiniam apvalkalui ir Delaunė trianguliacijai rasti galite panaudoti bet kokį laisvai platinamą kodą.
Pavyzdžiui galite panaudoti ir modifikuoti myDelaun.zip (~13 kb) kodą.
Literatūra