Boris Nikolajevic Delone

Delaunė trianguliacija

• Kas yra Delaunė trianguliacija?
• Taikymai
• Algoritmai
• Delaunė trianguliacija ir Voronojaus diagrama
• Praktinis darbas
• Literatūra

Kas yra Delaunė trianguliacija?

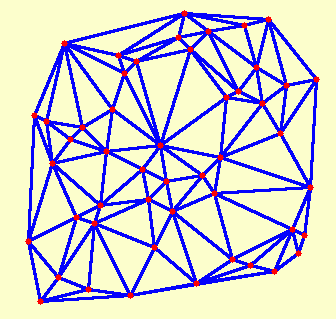
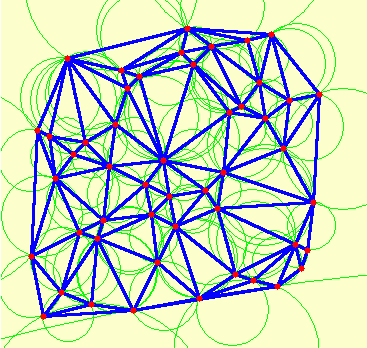
1-2 paveikslėlis. Plokštumos taškų Delaunė trianguliacija

Delaunė (Delaunay) trianguliacija vadinama toks plokštumos taškų M_i trejetų sujungimas trikampiais, kad nubrėžtame per bet kurio trikampio viršūnes apskritimo viduje nėra nei vieno taško M_i.

Delaunė trianguliacija padalina plokštumos sritį į trikampius. Delaunė trianguliacijos sąvoką galima apibendrint daugiamačiu atveju. Pavyzdžiui trimačiai M_i taškai yra talpinami į tokių tetraedrų viršūnes, kad nubrėžtos per bet kurio teatraedro viršūnes sferos viduje nėra nei vieno taško M_i.

Delaunė trianguliacija yra duali Voronojaus (Voronoi) diagramai.

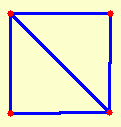
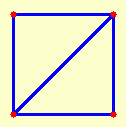
3-4 paveikslėlis. Stačiakampio viršūnių dvi galimos skirtingos Delaunė trianguliacijos

Jei tarp M_i taškų atsiras keturi ir daugiau taškų per kuriuos galima nubrėžti apskritimą kurio viduje nėra kitų taškų, tai tokių taškų aibei Delaunė trianguliaciją galima atlikti nevienareikšmiškai. Pateiktas paveikslėlis iliustruoja paprasčiausią nevienareikšmės Delaunė trianguliacijos atvejį kai duoti trianguliacijai keturi taškai yra plokštumos stačiakampio viršūnės. Nevienareikšmė Delaunė trianguliacija galima tik tokiu "išsigimusių" duomenų atveju ir todėl praktiškai ji pasitaiko retai. "Išsigimusių" duomenų atveju galima nežymiai pakeisti daugiau nei trijų vienam apskritimui priklausančių taškų koordinates taip, kad modifikuotiems duomenims gautųsi vienareikšmė Delaunė trianguliacija.

Taikymai

Delaunė trianguliacija (DT) yra taikoma:

• Kartografijoje, miestų planavime
• Planuojant mobiliųjų telefonų retransliacijos stočių išdėstymą
• Efektyviai artimiausiojo kaimyno paieškai (atpažinimas, kompiuterinė rega)
• Aproksimuojant paviršius (kompiuterinė geometrija, atpažinimas)
• Formuojant gardeles, baigtinių elementų metode (diferencialinės lygtys)
• Vizualizacijoje (kompiuterinė rega, geometrija)
• Daugiamačių duomenų struktūrose (kompiuterija)

Čia išvardinome tik keletą DT taikymo pavyzdžių. Kodėl DT yra taip plačiai taikoma? Tam tikra prasme DT yra artima rūšiavimui.

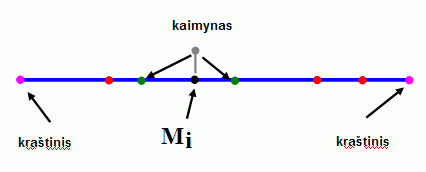
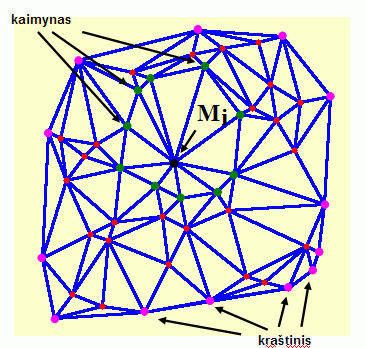
5-6 paveikslėlis. Vienmačių ir dvimačių duomenų "sutvarkymas"

Surūšiavus skirtingus viemačius (tiesės) taškus (pvz. didėjimo tvarka) kiekvienam taškui (išskyrus mažiausiąjį ir didžiausiąjį) surandame jo kaimynus. Taško M_i kaimynas iš kairės yra didžiausias iš mažesnių už jį, o kaimynas iš dešinės yra mažiausias iš didesnių už jį. "Kairės" ir "dešinės" sąvokos yra susitarimo reikalas; po rūšiavimo gautus taško kaimynus galėjome pavadinti "pirmu" ir "antru" kaimynu.

Žinia dvimačius (plokštumos) taškus surūšiuoti "didėjimo" ar "mažėjimo" tvarka negalima. Tačiau žiūrint į rūšiavimo rezultatą surandamų kaimynų prasme šią procedūrą galima apibendrinti ir daugiamačių taškų atveju. Tuo tikslu atliekama daugiamačių taškų Delaunė trianguliaciją. Apibrėžtumo dėklei tarkime, kad M_i yra dvimačiai (plokštumos) taškai. Apibendrinsime taško "pirmojo" ir "antrojo" kaimyno sąvoką plokštumos taško M_i kaimynais pavadindami aibę visų viršūnių, kurios pasiekiamos viena trianguliacijos tiesės atkarpa iš taško M_i.

Dėl "kairės" ir "dešinės" plokštumos atveju taip pat galime susitarti. Tuo tikslu taško M_i kaimynus sunumeruojame taip, kad numerio didėjimo tvarka žiūrint iš "centrinio" taško M_i jie būtų išsidėstę pagal laikrodžio rodyklę.

Vienmatis "mažiausias" arba "didžiausias" taškas yra kraštinis. Plokštumos tašką M_i vadinsime kraštiniu, jei iš trianguliacijos atkarpų, kurių abi viršūnės yra taško kaimynai, nesusidarys uždaras kontūras.

Delaunė trianguliacijos taikymas taškų retinimui ir artmiausiojo kaimyno paieškai. Pavyzdžiui toks uždavinys natūraliai kyla grupuojant pirštų atspaudų požymius ("minutes").

                                   

Piršto atspaudo pradinis vaizdas , "Meksikietiška skrybėle" filtruotas pirštas, ekstremalių taškų kontūrai.

Delaunė trianguliacija neblogai tinka mastelio keitimui. Pvz. vienmačiu atveju taškus galima surūšiuoti reikšmių didėjimo arba mažėjimo tvarka ir išmesti kas antrą. Kadangi Delaunė trianguliacija apibrėžia vieną plokštumos taškų rūšiavimo būdų, galime elgtis analogiškai. Iš duotųjų plokštumos taškų pasirenkame tokius, kad atstumas tarp jų būtų dvi Delaunė trianguliacijos kraštinės. Likusiems taškams galima vėl atlikti Delaunė trianguliaciją ir kartoti procedūrą rekurentiškai. Gausime hierarchinę pradinių taškų išretinimo struktūrą.

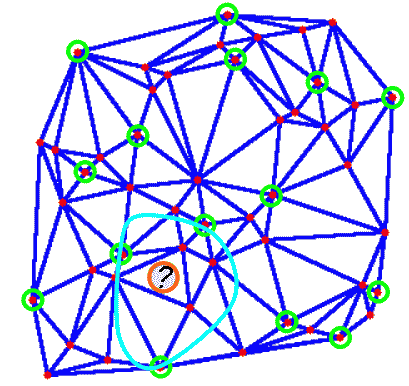
Panaudojant hierarchinę taškų išretinimo struktūrą galime greitai rasti koks yra artimiausias taškas iš pradinės taškų aibės bet kokiam duotam (tačiau iš anksto nežinomam) plokštumos taškui. Fiksuotas taškas, kuriam norime rasti "artimiausią kaimyną", paveikslėlyje pažymėtas klaustuku. Iš pradžių rasime kokiam trianguliacijos trikampiui priklauso duotasis taškas stambiausioje Delaunė trianguliacijoje, o po to rekurentiškai tikslinsime vietą mažinant mastelį. Radus kokiam smulkiausio mastelio trianguliacijos trikampiui priklauso taškas, pakaks apskaičiuoti atstumus iki trijų to trikampio viršūnių ir išsirinkti iš trijų taškų tašką su mažiausia atsumo reikšme. Aprašyto artimiausiojo kaimyno paieškos algoritmo sudėtingumas yra O(log N), kas žymiai geriau nei O(N) tiesioginio paieškos algoritmo, kai skaičiuojami atstumai iki visų taškų ir išrenkamas taškas su mažiausia atstumo reikšme. Kadangi Delaunė trianguliacijos sudėtingumas yra didesnis nei O(N), tokią schemą tikslinga taikyti, jei reikia rasti greitai atstumą iki daugelio nežinomų iš anksto taškų.

Algoritmai

Ieškant Delaunė trianguliaciją svarbu sudaryti patogias taškų, kraštinių ir trikampių duomenų struktūras bei mokėti greitai patikrinti ar plokštumos taškas D=(D_x,D_y) priklauso apskritimo nubrėžto per taškus A=(A_x,A_y), B=(B_x,B_y) ir C=(C_x,C_y) viduje. Jei taškai A,B ir C sutvarkyti (sužymėti) taip, kad jie guli apskritime prieš laikrodžio rodyklę, tai D bus apskritimo viduje tada ir tik tada kai matricos  

A_x   A_y   A_x² + A_y²   1

B_x   B_y   B_x² + B_y²   1

C_x   C_y   C_x² + C_y²   1

D_x   D_y   D_x² + D_y²   1
 
determinantas bus teigiamas.

Bet kokios plokštumos taškų aibei galima atlikti Delaunė trianguliaciją. Galimas toks tiesioginis M₀, M₁, ..., M_N-1 taškų Delaunė trianguliacijos algoritmas.

    for (int i=0; i<N-2; i++) 
	for (int j=i+1; j<N-1; j++) 
	   for (int k=j+1; k<N; k++){
		// Rasti apskritimą kertantį taškus Mi, Mj, Mk
				...
		for (int l=0; l<N; l++){
		// Tikrinti ar Ml taškas nėra apskritimo viduje

				...

		// Jei visi Ml taškai nėra apskritimo viduje
		// papildyti trianguliaciją (Mi,Mj,Mk) trikampiu

				...
		}
	   }

Šio tiesioginio DT algoritmo sudėtingumas yra O(N⁴). Trumpai apibūdinsime keletą efektyvesnių DT algoritmų.

1. Keitimo [1] algoritmas pradedamas nuo bet kokios trianguliacijos, kuri yra nuosekliai konvertuojama į Delaunė trianguliaciją.
   
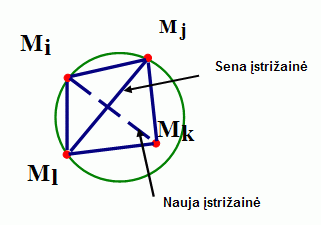
   Keturkampio [M_i,M_j,M_k,M_l], sudaryto iš dviejų gretimų trianguliacijos trikampių [M_i,M_j,M_l] ir [M_j,M_k,M_l], įstrižainė [M_j,M_l] keičiama į [M_i,M_k], jei viršūnė M_k yra apskritimo, kertančio trikampio [M_i,M_j,M_l] viršūnes, viduje. Tokiu būdu ([M_i,M_j,M_l], [M_j,M_k,M_l]) trikampių pora keičiama į ([M_i,M_j,M_k],[M_k,M_l,M_i]) porą.
2. Atsitiktinio įterpimo algoritmas [2] trianguliaciją pradeda nuo trijų apjungtų trikampiu taškų pasirenkant atsitiktinai sekantį tašką, kuris prijungiamas prie trianguliacijos. Ši procedūra kartojama kol išsemiami visi taškai. Trianguliacijos papildymas atliekamas panaudojant ketvirtainį, aštuntainį arba Delaunė medį.
3. Nuoseklaus trianguliacijos papildymo algoritmas papildo dalinę trianguliaciją nauju trikampiu. Delaunė trikampių sparti paieška atliekama panaudojant reguliarią gardelę [3] ir išretintą matricą [4].
4. "Skaldyk ir valdyk" algoritmas [5] rekursyviai atlieka į dvidalis dalinamas taškų Delaunė trianguliacijas. Yra sugalvoti efektyvūs trianguliuotų dalių apjungimo algoritmai.
5. "Šluojančios tiesės" (angl. sweepline) yra vienas žinomiausių ir efektyviausių DT algoritmų. Šį algoritmą atrado S.Fortune [6],[7]. Algoritmo pradžioje plokštumos taškai yra sunumeruojami taškų abscisių didėjimo tvarka. Trianguliacija atliekama nuosekliai papildant taškais su didėjančiomis abscisėmis. Vizualiai tokį trianguliacijos taškų papildymą galima vaizduoti iš kairės į dešinę judančia vertikalia tiese iš ko ir kilo metodo pavadinimas. Algoritmo sudėtingumas yra O(Nlog(N)). Čia N - trianguliuojamų plokštumos taškų skaičius.
6. "Projekcinis algoritmas" remiasi tokia geometrijos teorema.

   Teorema. Plokštumos taškų Delaunė trianguliacija yra projekcija į x-y plokštumą apatinės iškilos trimatės srities, gaunamos surandant erdvės taškų (x_i,y_i,(x_i)²)+(y_i)²) iškilą apvalkalą.

   Tiesioginė šio algoritmo realizacija yra O(N⁴) sudėtingumo. Tiesioginio algoritmo schema būtų tokia.

   
   for ( i=0; i<N; i++) zi = (xi)2 + (yi)2;
   for ( i=0; i<N-2; i++){
       for ( j=0; j<N-1; j++){
   	for ( k=0; k<N; k++){
               	Apskaičiuoti trikampio normalę
               	Surandame apatinius trikampius
               	for ( m=0; m<N; m++){
                       jei taškas m yra virš trikampio apibrėžiamo indeksais (i,j,k),
                            tai trikampis lieka Delaunė trianguliacijos kandidatu;
                       priešingu atveju baigti tikrinimą, nes (i,j,k) indeksais
   			apibrėžiamas trikampis nepriklauso Delaunė trianguliacijai.
                   }
   	}
       }
   }
   
   

   Organizuojant subtiliau tikrinimus šio algoritmo sudėtingumą galima sumažinti iki O(N²).
7. Gaubiančiojo trikampio algoritmas pirma suranda pakankamai didelį trikampį, kuris nekeičia vidinių taškų trianguliacijos. Po to atsitiktinai paeiliui parenkami dar neprijungti taškai ir pataisoma ankstesniame žingsnyje rasta Delaunė trianguliacija. Realizavus efektyvią paiešką kokiam trikampiui priklauso naujai pasirinktas taškas galima pasiekti, kad gaubiančiojo trikampio algoritmo sudėtingumas būtų O(N ln(N)).
8. Pasiūlysime dar vieną O(N²) sudėtingumo algoritmą.
   • Pirma surandame plokštumos taškų iškilą apvalkalą. Taikant "skaldyk ir valdyk" principą iškilą apvalkalą rasime atlikę O(N ln(N)) operacijų.
   • Surandame atkarpas einančias per kraštinius rasto iškilo apvalkalo taškus. Šias atkarpas įtraukiame į Delaunė trianguliaciją.
   • Pasirenkame vieną iš kraštinių atkarpų ir ieškome viršūnės tinkamos suformuoti Delaunė trianguliacijos trikampį, kurio viena kraštinių būtų pasirinktoji. Šią procedūrą kartojame kol bus pilnai suformuota Delaunė trianguliacija.
   
   

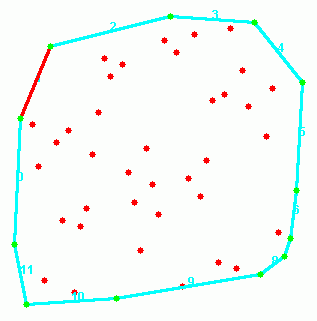
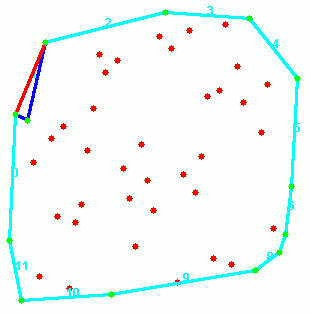
   8-9 paveikslėlis. Algoritmo trečiojo žingsnio pirmoji iteracija
   

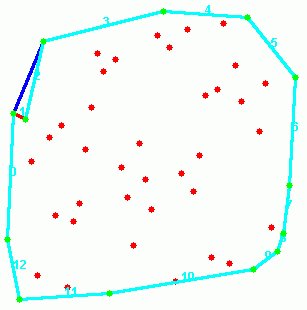
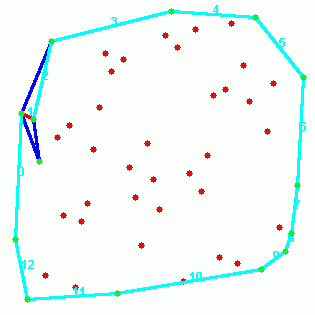
   10-11 paveikslėlis. Algoritmo trečiojo žingsnio antroji iteracija
   

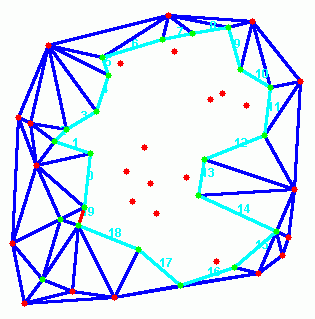
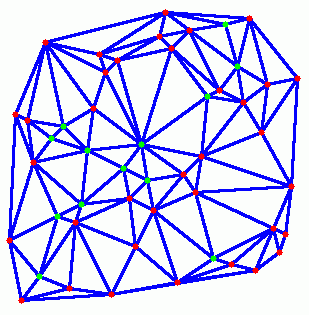
   12-13 paveikslėlis. Algoritmo trečiojo žingsnio 50-oji ir 104-oji iteracija

   Kadangi Delaunė trianguliacijoje yra O(N) atkarpų, o tiesioginei DT tinkamos viršūnės paieškai reikia atlikti O(N) operacijų, bendras algoritmo sudėtingumas yra O(N ln(N)) + O(N²).
   Šio algoritmo sudėtingumą galima dar sumažinti atsisakant tiesioginės tinkamos pasirinktai atkarpai viršūnės paieškos.

Delaunė trianguliacija ir Voronojaus diagrama

Plokštumos taškų M_i Voronojaus (Voronoi) diagrama vadiname plokštumos suskaidymą į sritis, pasižyminčias savybe, kad sričiai priklausantis taškas M_i yra artimiausias visiems tos srities taškams.

Pateiksime Voronojaus diagramos taikymo. Pažymėkime plokščiame žemėlapyje visus pasaulio šulinius ir nuspalvinkime skirtingomis spalvomis žemėlapyje sritis, kuriose būnant keliautojui būtų artimiausias šulinys toje srityje esantis šulinys. Šią problemą išsprendžia Delaunė trianguliacija.

Delaunė trianguliacija yra duali Voronojaus diagramai. Voronojaus diagramą iliustruoja 14 paveikslėlis, o dualumo sampratą 15 paveikslėlis.


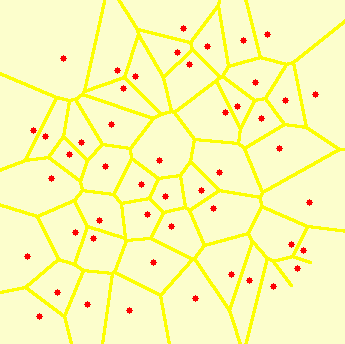
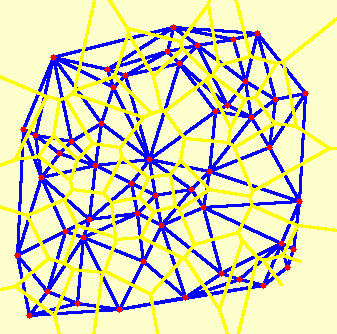
14-15 paveikslėlis. Plokštumos taškų Voronojaus diagrama ir jos dualumas Delaunė trianguliacijai.

Žinant Delaunė trianguliaciją, Voronojaus diagramą galima surasti atlikus O(N ln(N)) veiksmų. Norint tai padaryti reikia iš Delaunė trianguliacijos atkarpų vidurių iškelti statmenis ir rasti statmenų suformuojamą plokštumos suskaidymą.

Praktinis darbas

Realizuokite Delaunė trianguliacijos algoritmą Java kalba.
Jūsų algoritmas bus vertinamas pagal atlikimo greitį.
Duomenis testavimui generuokite tokiu metodu:

public static int[] randperm(int n,int[] j0){
 Random R=new Random(n+((long)n)<<31);
 int[] j = new int[n];
 int w,k;
 if (j0==null)	for (int i=0; i<n; i++) j[i]=i;
	else	for (int i=0; i<n; i++) j[i]=j0[i];
 for (int i=0; i<n; i++) {
	w=(int)(n*R.nextDouble());
	if (w==n) w=n-1;
	k=j[i]; j[i]=j[w]; j[w]=k;
 }	
 return j;
}

Siekiant efektyvumo galite laikyti, kad Delaunė trianguliacija atliekama specifiniams duomenims, kurių taškų koordinatės yra sveiki skaičiai gaunami atsitiktinai perstatant seką {0,1,2,...,N-1}.
Šis puslapis iliustruotas su duomenimis

	int N=49;
	int[] x=randperm(N,null),	y=randperm(N,x);

kuriuos patartina naudoti derinant ir testuojant Delaunė trianguliacijos algoritmą.

Jūsų klasė turi praplėsti (extends) delaune paketo Delaune klasę.

Delaune paketo kodas: delaune.jar (1374 baitai).

karalevicius.jar (11866 baitai) archyve rasite Raimundo Karalevičiau atliktą užduotį, kuri buvo testuojama su
Test.java klase (java Test komanda).

Literatūra  
 


1. R.Sibson. Locally equiangular triangulations. The Computer Journal Vol.2 (3): 243-245, 1973.
2. L.J.Guibas, D.E.Knuth and M.Sharir. Randomized Incremental Construction of Delaunay and Voronoi diagrams. Algorithmica 7: 381-413, 1992.
3. T.Fang and L.Piegl. Delaunay triangulation using a uniform grid. IEEE Computer Graphics and Applications: 36-47, 1993.
4. T.Fang and L.Piegl. Algorithm for Delaunay triangulation and convex hull computation using a sparse matrix. Computer Aided Design Vol.24(8): 425-436, 1992.
5. P.Cignoni, C.Montani, R.Perego and R.Scopigno. Parallel 3D Delaunay Triangulation. Eurographics 93: 129-142, 1993.
6. S.Fortune. Sweepline Algorithms for Voronoi diagrams. Algorithmica 2: 153-174, 1987.
7. Čuk Roman. Construction of Voronoi diagrams using Fortune's method : A look on an Implementation
8. Alper Üngör "Sweep line" algoritmo java realizacija
9. Gaubiančio trikampio algoritmas