1. Atpažinimo sistemos kokybės įvertinimas ir jo vizualizacija
- Atpažinimo kokybės įvertinimas
- Verifikavimo kokybės vizualizacija
- Identifikavimo kokybės įvertinimo vizualizacija
- Praktinė ROC kreivė
- Praktinė užduotis
- Projektas
- Literatūra
1.1. Atpažinimo kokybės įvertinimas
Atpažinimo sistemos kokybės įverčio principus aiškinsimės paprastais atvejais kai atpažinimui yra pateikiamos objektas ar objektų pora ir atpažinimo sistemai reikia priimti binarinį sprendimą patvirtinantį arba paneigiantį teiginį, kad objektas priklauso vienai klausei ar jai nepriklauso ir ar poros objektai yra tos pačios klasės atstovai. Toks porų atpažinimo uždavinys biometrikoje vadinamas verifikavimu (angl. verification). Tarkime sistemai pateikiamos dvi skaitmeninės veidų nuotraukos ( nuotrauka x ir nuotrauka y ) ir atpažinimo sistemai reikia patvirtinti ( verifikuoti ), kad dvi nuotraukos yra to paties asmens (priklauso tai pačiai vieno asmens visų galimų nuotraukų klasei). Biometrinės asmenų tapatybės verifikavimo sistemai dažniausiai pateikiama veidų, pirštų atspaudų, delnų, ar akies rainelių skaitmeninių vaizdų pora ir sistema turi priimti autonominį sprendimą ar pateiktų objektų pora yra vieno asmens ar ne. Apibrėžtumo dėlei laikysime, kad atpažinimo sistema kiekvienai duotajai vaizdų porai ( x, y ) priskiria vienetą, jei sistema priėmė sprendimą, kad poros ( x, y ) nuotraukos x ir y yra to paties individo. Priešingu atveju, kai priimamas sprendimas, kad nuotraukos x ir y yra skirtingų asmenų, sistema porai ( x, y ) priskiria nulį. Vadinasi binarinis atpažinimas ekvivalentus atvaizdžiui
![]()
Kiek kitokia binarinio atpažinimo ( klasifikavimo ) esmė medicininiuose taikymuose. Čia taip pat dažniausiai reikalaujama priimti binarinį sprendimą: pacientas duota liga serga / neserga 1/0, tačiau šiuo atveju dažnai atpažinimui pateikiamas tik vienas objektas, pvz. skaitmeninė elektrokardiograma (EKG) ar tomografijos skenavimo skaitmeninių vaizdų seka. Šiuo atveju atpažinimo sistema priima sprendimą lyginant duotąjį objektą x ( elektrokardiogramą, tomografijos vaizdų seką ) su turimais ankstesniais pavyzdžiais y, kuriems yra žinoma ar jų šaltinis priklausė sergančių ar nesergančių asmenų grupei. Formaliai binarinis atpažinimas medicininėse aplikacijose dažnai gali būti išreikštas funkcija

Ir vienu ir kitu atveju vertinant atpažinimo kokybę yra
postuluojama, kad disponuojame absoliučiai teisinga verifikuojamos poros ![]() ar informacijos
ar informacijos ![]() klasifikavimo
informacija. Taigi binarinio atpažinimo/klasifikavimo sistema kiekvienai porai
ar objektui priskiria 1 arba 0 ir tai pačiai porai ar objektui yra žinoma
teisinga reikšmė: 1 arba 0. Viso gali susidaryti keturi skirtingi atvejai: (1,1),
(1,0), (0,1) ir (0,0). Atpažinimo kokybės prasme (1,1) ir (0,0) atvejai yra
teigiami. Pvz. medicininiame kontekste (1,1) atitinka atvejį, kai atpažinimo
sistema remiantis pateikta skaitmenine informacija x priėmė sprendimą,
kad x duomenų šaltinis serga duota liga ir šis sprendimas buvo
teisingas. (0,0) atveju sistema priėmė sprendimą, kad duomenys x
priklauso nesergančiam liga asmeniui ir šis sprendimas taip pat buvo teisingas.
Likę atvejai (1,0) ir (0,1) žymi dvi skirtingas atpažinimo klaidas: (1,0)
sistema klaidingai priėmė sprendimą apie ligą, nors asmuo ja nesirgo, ir
atvirkščiai (0,1) atveju sistema suklydo teigdama, kad asmuo duota liga
neserga, nors iš tikrųjų jis ja serga. Verifikacijos atveju galimų sprendimų
porų interpretacija tokia:
klasifikavimo
informacija. Taigi binarinio atpažinimo/klasifikavimo sistema kiekvienai porai
ar objektui priskiria 1 arba 0 ir tai pačiai porai ar objektui yra žinoma
teisinga reikšmė: 1 arba 0. Viso gali susidaryti keturi skirtingi atvejai: (1,1),
(1,0), (0,1) ir (0,0). Atpažinimo kokybės prasme (1,1) ir (0,0) atvejai yra
teigiami. Pvz. medicininiame kontekste (1,1) atitinka atvejį, kai atpažinimo
sistema remiantis pateikta skaitmenine informacija x priėmė sprendimą,
kad x duomenų šaltinis serga duota liga ir šis sprendimas buvo
teisingas. (0,0) atveju sistema priėmė sprendimą, kad duomenys x
priklauso nesergančiam liga asmeniui ir šis sprendimas taip pat buvo teisingas.
Likę atvejai (1,0) ir (0,1) žymi dvi skirtingas atpažinimo klaidas: (1,0)
sistema klaidingai priėmė sprendimą apie ligą, nors asmuo ja nesirgo, ir
atvirkščiai (0,1) atveju sistema suklydo teigdama, kad asmuo duota liga
neserga, nors iš tikrųjų jis ja serga. Verifikacijos atveju galimų sprendimų
porų interpretacija tokia:
1.
(1,1) atpažinimo sistema priėmė teisingą
sprendimą, kad biometriniai duomenys ![]() yra to paties asmens;
yra to paties asmens;
2.
(1,0) atpažinimo sistema priėmė klaidingą
sprendimą, kad biometriniai duomenys ![]() yra to paties asmens;
yra to paties asmens;
3.
(0,1) atpažinimo sistema priėmė klaidingą
sprendimą, kad biometriniai duomenys ![]() yra skirtingų asmenų;
yra skirtingų asmenų;
4.
(0,0) atpažinimo sistema priėmė teisingą
sprendimą, kad biometriniai duomenys ![]() yra skirtingų asmenų.
yra skirtingų asmenų.
Vertinant atpažinimo kokybę atliekamas atpažinimas turimos dokumentuotos[1] duomenų bazės sudaroma 2x2 skaičių lentelė, kurioje įrašoma (1,1), (1,0), (0,1) ir (0,0) atvejai:
![]() .
.
Šiuo metu jau nusistovėjo kiekvieno matricos langelio angliški terminai, kurių ir mes laikysimės. Medicininiame kontekste #(1,1) langelio skaitliukas vadinasi True Positive (TP) skaičiumi, #(1,0) False Positive (FP), #(0,1) False Negative (FN), #(0,0) True Negative (TN). Tarkime kompiuteriniu algoritmu buvo analizuojamos skaitmeninės kardiogramos tikslu diagnozuoti miokardo infarktą. Laikoma, kad tuos pačius duomenis ir kitą medicininę informaciją analizavo medikų grupė ir priėmė absoliučiai teisingus sprendimus kokios EKG priklauso pacientams su miokardo infarktu, o kokios ne. Tiesą sakant realiai labai tikslios skiriamosios ribos tarp infarkto ir neinfarkto nėra. Pvz. mikroinfarkto atveju apmiršta tik maža širdies raumens dalis ir kokiai grupei priskiriamas pacientas yra gana subjektyvus sprendimas. Panagrinėkime pavyzdį. Tarkime viso atpažinimui buvo pateikta 340 elektrokardiogramų, iš kurių 115 priklausė pacientams su miokardo infarktu (MI). Tuomet viena galimų 2x2 skaičių lentelė galėtų būti tokia:
![]() .
.
Fiksavus pacientų skaičių su MI (mūsų atveju 115 ) ir be MI ( mūsų atveju 340 115 = 225 ) skirtingi atpažinimo algoritmai keturių skaičių lentelėje nulems tik du nepriklausomus skaičius #FN ir #FP, o likę du turės tenkinti lygtis
![]()
Standartizuojant atpažinimo kokybės įvertį 2x2 matricos stulpeliai yra normuojami ( padalinami ) iš #TP + #FN = #P ir #FP + #TN = #N skaičių ir taip gaunama dažnių lentelė. Mūsų pavyzdžio atveju gausime tokias reikšmes
![]()
Paskutinis žymėjimų simbolis F skaitomas Frequency dažnis.
Pavyzdžiui, TPF True Positive Frequency. Normuotose dažnių lentelėse visi
keturi elementai yra neneigiami ir nedidesni už 1, pirmojo ir antrojo stulpelių
elementų suma lygi 1, pirmosios ir antrosios eilutės elementų suma gali kisti
nuo 0 iki 2 ir visų keturių matricos elementų suma visuomet lygi 2. Bendras
atpažinimo kokybės vertinimo principas yra toks kuo labiau normuotos 2x2
atpažinimo dažnių matricos įstrižainės elementai labiau dominuoja (didesni),
tuo geresnė atpažinimo kokybė. Deja tik nesudėtingų duomenų atveju
pavyksta atlikti idealų atpažinimą, kurio dažnių lentelė yra: ![]() (ideali). Nenaudojant
jokio atpažinimo algoritmo galima postuluoti, kad visi serga arba visi
sveiki ir gauti trivialias dažnių lenteles
(ideali). Nenaudojant
jokio atpažinimo algoritmo galima postuluoti, kad visi serga arba visi
sveiki ir gauti trivialias dažnių lenteles![]() (optimisto strategijos visi sveiki
atpažinimo kokybės dažnių lentelė) ir
(optimisto strategijos visi sveiki
atpažinimo kokybės dažnių lentelė) ir ![]() (pesimisto strategija visi serga).
Pateiktos dažnių lentelės yra kraštiniai atvejai. Šiuolaikinių atpažinimo
algoritmų sprendimai dažniausiai priklauso nuo pasirinkto slenksčio ir tokiu
būdu algoritmo vartotojas gali pasirinkti atpažinimo kokybės lentelę
optimizuodamas pageidaujamus parametrus. Medicininių klasifikavimo algoritmų
atveju keliami aukšti reikalavimai FPF parametrui. Kitais žodžiais
tariant siekiama, kad sistema retai klystų pripažindama sergančiu kokia nors
liga asmenį, nors jis iš tikrųjų ta liga neserga.
(pesimisto strategija visi serga).
Pateiktos dažnių lentelės yra kraštiniai atvejai. Šiuolaikinių atpažinimo
algoritmų sprendimai dažniausiai priklauso nuo pasirinkto slenksčio ir tokiu
būdu algoritmo vartotojas gali pasirinkti atpažinimo kokybės lentelę
optimizuodamas pageidaujamus parametrus. Medicininių klasifikavimo algoritmų
atveju keliami aukšti reikalavimai FPF parametrui. Kitais žodžiais
tariant siekiama, kad sistema retai klystų pripažindama sergančiu kokia nors
liga asmenį, nors jis iš tikrųjų ta liga neserga.
1.2. Verifikavimo kokybės vizualizacija
Verifikacijos atveju terminai nėra galutinai nusistovėję, tačiau atpažinimo dažnių lentelėje dažniausiai naudojami tokie žymėjimai:
![]()
TAR teisingo pripažinimo (True Acceptance Rate) dažnis,
FAR klaidingo pripažinimo (False Acceptance Rate) dažnis,
FRR klaidingo atmetimo (False Rejection Rate) dažnis,
TRR teisingo atmetimo True Rejection Rate dažnis.
Paryškinti terminai žymi atpažinimo klaidas ir jų reikšmės naudojamos vizualizuojant atpažinimo algoritmo kokybę. Realiai atpažinimo sistemos priima sprendimus remiantis pateiktų verifikacijai objektų x ir y panašumo (angl. similarity) arba atstumo (angl. distance) įverčiu. Naudojant atstumo įvertį objektų pora laikoma tuo panašesne, kuo atstumas tarp jų mažesnis. Panašumo įverčio atveju atvirkščiai kuo panašumo įvertis didesnis, tuo objektai panašesni. Principinio skirtumo tarp pasirinkimo naudoti panašumo ar atstumo įverčius nėra, todėl toliau mes fiksuosime vieną jų, būtent - atstumą. Tipinė verifikavimo schema yra tokia.
1. Pasirenkama sprendimo priėmimo slenksčio reikšmė trshld>0.
2. Apskaičiuojamas atstumas tarp lyginamos objektų poros:
![]()
3. Primamas sprendimas:
![]()
Tokiu būdu pilnai atpažinimo algoritmą charakterizuoja ne viena 2x2 atpažinimo dažnių matrica, bet tokių matricų aibė gaunama renkantis visas galimas slenksčio reikšmes. Todėl naudojant patikslintus žymėjimas reikia rašyti ne FAR ar FRR, o
![]() .
.
Čia t žymi slenksčio trshld reikšmę. Kadangi praktiškai dažnių lentelė gaunama iš baigtinio skirtingų galimų lyginti porų, tai yra tik baigtinis skaičius skirtingų slenksčio reikšmių, su kuriomis gaunasi skirtingos atpažinimo dažnių lentelės. Atpažinimo kokybės vizualizacijos idėja labai parasta yra piešiama parametrinė {FRR(t), FAR(t)} grafiko kreivė. Abscisių ašyje atidedamos FAR(t) klaidingo pripažinimo (false acceptance), o ordinačių FRR(t) klaidingo atmetimo (false rejection) dažniai (rates). Dominuoja du gaunamos kreivės angliški vadinamai: DET (Detection Error Trade-off) ir ROC (Receiver Operating Characteristic) kreivė. DET pavadinamas kartais siejamas su variantu, kai grafikas piešiamas logaritminėje skalėje, tačiau kartais skirtumas tarp šių kreivių yra esminis: ROC kreivės atveju ordinačių ašyje atidedama ne FRR(t), o TRR(t) reikšmė.
Paanalizuokime kokie galimi binarinio atpažinimo teisingų ir klaidingų sprendimų vizualizacijos variantai.
Fiksavus algoritmo sprendimo slenkstį t, turime keturis dažnius:
TAR(t) FAR(t)
FRR(t) TRR(t)
Gauname 2x2 skaičių matricą, kurios įstrižainėje yra teisingų sprendimų dažniai, o šalutinėje įstrižainėje
klaidingų sprendimų dažniai. Pasirinkę kokią nors dviejų dažnių porą ir keičiant sprendimo slenksčio reikšmes t
gauname parametrinę kreivę, kuri ir vizualizuoja atpažinimo algoritmo sprendimų tikslumą. Neskiriant simetrinių variantų (pvz. (FAR(t),TAR(t)) ir (TAR(t),FAR(t)) yra simetriniai ),
galimi šeši skirtingi variantai:
Kaip jau pastebėjome, literatūroje dažniausiai sutinkami du pasirenkamų dažnių porų variantai:
- (FAR(t),FRR(t)), DET arba ROC kreivė.
- (FAR(t),TAR(t)). ROC kreivė. Medicinos taikymuose TAR dažnai vadinamas jautrumu (sensitivity), o FAR = 1 - TRR = 1 - specifiškumas ( 1 - specificity ).
Keletas interneto nuorodų į ROC ir DET kreives, atkreipkite dėmesį kaip tiems patiems dalykams įvardinti skiriasi terminija.
Šaltinis: Fawcett (2004). |
Mes nelietuvinsime angiškųjų pavadinimų ir visais atvejais naudosime ROC (FAR(t),FRR(t)) variantą.
Šis variantas dažnai naudojamas vertinant pirštų atspaudų atpažinimo algoritmų kokybę.
Taigi ROC kreivė grafiškai vizualizuoja atpažinimo algoritmo kokybę.
Kuo ROC kreivė yra žemiau tuo atpažinimo kokybė geresnė.
Jei dviejų skirtingų algoritmų ROC kreivių grafikai kertasi
vienareikšmiai pasakyti kuris atpažinimo algoritmas yra geresnis negalima.
Idealaus atpažinimo kreivė sutampa su abscisių ašimi. Esant aukštos kokybės
atpažinimui dažnai naudojamos logaritminės ašys. Taip yra vizualizuojami ir atstumų dist(x,y) = t tankis,
t.y. abscisių ašyje atidedama slenksčio t reikšmė, ordinačių ašyje
dažnis su kuriuo pasitaiko dist(x,y) = t reikšmė. Tankiai yra vizualizuojami
atskirai autentiškų ( angl. genuines ) ir apsišaukėlių (
angl. impostors) porų aibėms Formalizuokime įvestus terminus, kad būtų galima įžvelgti sąsajas su
žinomomis tikimybių teorijos sąvokomis. Pažymėkime Šiose formulėse pradedame integruoti nuo 0, kadangi darome prielaidą,
kad atstumo reikšmė negali būti neigiama. Pateiksime analitinė pavyzdį, kuriame galima tiksliai apskaičiuoti
tankių ir dažnių reikšmes bei nupiešti ROC kreivę. Tankį o Kairiąją išraišką interpretuosime atstumo tankio išraiška autentiškoms
poroms kai taikomas pirmas atpažinimo algoritmas, analogiškai viduriniąją
išraišką susiesime su antruoju atpažinimo algoritmu ir dešiniąją su trečiuoju hipotetiniu
atpažinimo algoritmu ir bandysime išsiaiškinti koks atpažinimo algoritmas yra
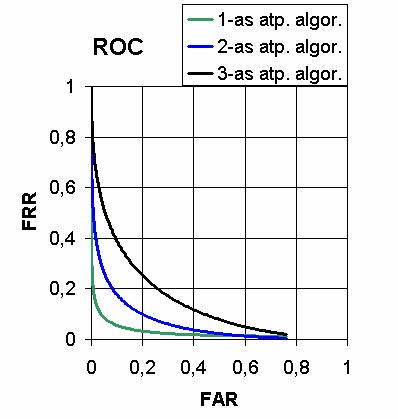
geriausias. Nesunku įsitikinti, kad 1
pav. p(t|H_1) ir trijų atpažinimo algoritmų tankiai p(t|H_0). 2 pav. Trijų atpažinimo algoritmų
ROC kreivės. Visų tankių grafikai iliustruoti 1 pav. Kitas paveikslėlis iliustruoja
trijų algoritmų ROC kreives. Kadangi pirmojo atpažinimo algoritmo ROC kreivė
žemiausia, šio algoritmo kokybė yra geriausias. Antrojo atpažinimo algoritmo
ROC kreivė yra viduryje, todėl jis atpažinimo kokybės prasme yra antroje
vietoje. Kadangi realių atpažinimo algoritmų ROC kreivės dažnai kertasi, joms
palyginti parenkami specifiniai taškai. Vienas, bene populiariausių, yra taip
vadinamas Zero FAR taškas. Šis taškas ROC kreivėje turi koordinates (0, FRR),
t.y. šiame ROC kreivės taške FAR reikšmė lygi 0. (0, FRR) taško FRR reikšmė
reiškia kokią dalį atpažinimo sistema atmeta autentiškų porų atmesdama visas
apsišaukėlių poras. Analogiškai apibrėžiamas Zero FRR taškas. ROC kreivės
taškas (FAR, 0) kokią dalį apsišaukėlių sistema praleidžia nedarydama nei
vienos neteisingo atmetimo klaidos. Abi šios charakteristikos kiek nestabilios,
nes priklauso nuo sistemai pateikiamų duomenų kiekio. Žymiai stabilesnis yra
Equal Error EER ROC kreivės taškas kurio abi koordinatės yra vienodos, t.y.
daroma vienodai FAR ir FRR klaidų. Plačiau apie ROC kreivę galite paskaityti [Wikipedia
ROC], [Magnificent ROC]. ![]() - nulinė hipotezė, kad lyginama
pora (x,y) yra autentiška.
- nulinė hipotezė, kad lyginama
pora (x,y) yra autentiška. ![]() žymėsime tikimybinio tankio
žymėsime tikimybinio tankio ![]() reikšmę esant teisingai
reikšmę esant teisingai![]() prielaidai. Simboliu
prielaidai. Simboliu ![]() žymėsime analogišką
tankį kai teisinga alternatyvi hipotezė
žymėsime analogišką
tankį kai teisinga alternatyvi hipotezė ![]() - lyginama pora nėra autentiška. Jeigu
atpažinimo algoritmas priima teisingų sprendimų daugiau nei klaidingų, tai
- lyginama pora nėra autentiška. Jeigu
atpažinimo algoritmas priima teisingų sprendimų daugiau nei klaidingų, tai ![]() grafiko didžiausios
reikšmės turėtų grupuotis arčiau minimalios atstumo reikšmės 0, o
grafiko didžiausios
reikšmės turėtų grupuotis arčiau minimalios atstumo reikšmės 0, o ![]() - atvirkščiai. Tarp
tankių
- atvirkščiai. Tarp
tankių ![]() ir
ir ![]() ir klaidingų sprendimų
dažnių
ir klaidingų sprendimų
dažnių ![]() ir
ir ![]() yra toks ryšys:
yra toks ryšys: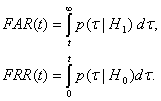
![]() fiksuosime:
fiksuosime:![]()
![]() apibrėžimui naudosime
vieną iš trijų išraiškų:
apibrėžimui naudosime
vieną iš trijų išraiškų:![]() arba
arba ![]() arba
arba ![]()
![]() tankio grafiko maksimumas yra taške t = 5, o
trijų
tankio grafiko maksimumas yra taške t = 5, o
trijų ![]() tankių
atitinkamai t = 0, t = 1 ir t = 2.
tankių
atitinkamai t = 0, t = 1 ir t = 2. 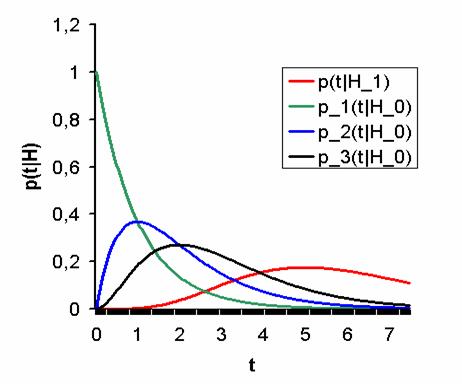
( 1, 50%), ( 2, 80%), ( 3, 100%), ( 4, 100%), ..., ( 10, 100%). 3 pav. iliustruoja vieno realaus algoritmo identifikavimo eiliškumo (CMC) kreivę. Eiliškumo kreivių panaudojimas turi savus apribojimus. Yra laikoma, kad visuomet lygiai viena iš N lyginamų porų yra autentiška. Galima bandyti apibendrinti CMC kreivės sąvoką tais atvejais, kai kelios lyginamos N poros yra autentiškos (poros biometriniai duomenys yra to paties asmens), tačiau kaip šiuo atveju apibrėžti poros identifikavimo vietą vienareikšmiškai neaišku. Vienas galimų variantų yra sugrupuoti saugyklos N įrašų grupėmis M ≤ N, kur M unikalių sagykloje asmenų kiekis, tačiau čia kyla klausimas kaip apibrėžti lyginimo su grupe panašumo taškų reikšmę. Ši problema ypač kebli, jei skirtingose grupėse gali būti skirtingas asmenų skaičius.

3 pav. Veidų atpažinimo vieno algoritmo CMC kreivė.
Sprendžiant praktinį ROC kreivės apskaičiavimo
uždavinį pirma reikia surasti tankių ir dažnių formulių praktinius atitikmenis.
![]() ir
ir ![]() praktiniai tankiai
randami sudarant dvi atstumų histogramas atskirai autentiškoms ir apsišaukėlių
poroms.
praktiniai tankiai
randami sudarant dvi atstumų histogramas atskirai autentiškoms ir apsišaukėlių
poroms.
Skaičiuojant praktines ROC kreives yra
fiksuojamas verifikacijos/atpažinimo algoritmas ir duomenų bazė, kuriai bus
taikomas šis algoritmas. Tarkime viso duomenų bazėje yra N įrašų ir ![]() yra bazės įrašai.
Atpažinimo algoritmas kiekvienai fiksuotai duomenų bazės porai
yra bazės įrašai.
Atpažinimo algoritmas kiekvienai fiksuotai duomenų bazės porai ![]() apskaičiuoja realų
skaičių
apskaičiuoja realų
skaičių ![]() .
Laikysime, kad šio skaičiaus interpretacija yra panašumas (s similarity).
Praktiniuose skaičiavimuose susitariama, kad panašumo galimos reikšmės yra
neneigiami sveikieji skaičiai galintys kisti nuo minimalios reikšmės
.
Laikysime, kad šio skaičiaus interpretacija yra panašumas (s similarity).
Praktiniuose skaičiavimuose susitariama, kad panašumo galimos reikšmės yra
neneigiami sveikieji skaičiai galintys kisti nuo minimalios reikšmės ![]() iki maksimalios
iki maksimalios ![]() . Jei lyginamos poros
panašumas ( angl. similarity ) lygus 0, tai reiškia kad tarp porą
sudarančių įrašų x_i ir x_j [2]
nerasta jokio panašumo ir atvirkščiai, atveju
. Jei lyginamos poros
panašumas ( angl. similarity ) lygus 0, tai reiškia kad tarp porą
sudarančių įrašų x_i ir x_j [2]
nerasta jokio panašumo ir atvirkščiai, atveju ![]() poros elementai yra maksimaliai panašūs.
Vertinant atpažinimo algoritmo kokybę būtina žinoti papildomą apriorinę
informaciją ar lyginama pora
poros elementai yra maksimaliai panašūs.
Vertinant atpažinimo algoritmo kokybę būtina žinoti papildomą apriorinę
informaciją ar lyginama pora ![]() yra autentiškų (angl. genuines
) ar apsišaukėlių (angl. impostors ). Kad šią informaciją
apibrėžti korektiškai kiekvienam duomenų bazės elementui x_i suteikiamus
identifikatorius id(x_i). Pavyzdžiui, jei įrašų duomenų bazės elementai yra
asmenų veidų nuotraukos, x_i identifikatorius galėtų būti nuotraukos
asmens vardas, pavardė ir jo asmens kodas. Praktiniuose skaičiavimuose patogiau
laikyti, kad identifikatorius taip yra sveikasis skaičius. Tokiu atveju pora
yra autentiškų (angl. genuines
) ar apsišaukėlių (angl. impostors ). Kad šią informaciją
apibrėžti korektiškai kiekvienam duomenų bazės elementui x_i suteikiamus
identifikatorius id(x_i). Pavyzdžiui, jei įrašų duomenų bazės elementai yra
asmenų veidų nuotraukos, x_i identifikatorius galėtų būti nuotraukos
asmens vardas, pavardė ir jo asmens kodas. Praktiniuose skaičiavimuose patogiau
laikyti, kad identifikatorius taip yra sveikasis skaičius. Tokiu atveju pora![]() yra autentiška tada ir
tik tada, kai
yra autentiška tada ir
tik tada, kai
id(x_i) = id(x_j).
Turint įrašus x_0, x_1, , x_(N-1) kyla klausimas kokias lyginamas poras sudaryti. Dažniausiai panašumo įverčiai būna simetriniai, t.y. visuomet s(x_i,x_j) = s(x_j,x_i). Todėl kaip taisyklė apskaičiuojami tokie panašumai:
s(x_0,x_1), s(x_0,x_2), , s(x_0,x_(N-1)),
s(x_1,x_2), s(x_1,x_3), , s(x_1,x_(N-1)),
.....
s(x_(N-2),x_(N-1)).
Tokiu būdu viso susidaro (N-1) + (N-2) + + 1 = N * (N-1) / 2 panašumo reikšmių.
.roc formatas.
Kad patogiau būtų lyginti ir naudotis failais,
kuriuose talpina informacija reikalinga apskaičiuoti ROC kreivei, susitarsime
dėl standartinio .roc failo formato. Laikysime, kad šiame faile įrašomi
tik sveikieji skaičiai binarine forma skiriant sveikajam skaičiui 4 baitus
ir išdėstant juos reikšmingumo didėjimo tvarka, t.y. pirmasis iš 4 baitų yra
jauniausiasis, o paskutinis 4 asis vyriausiasis ( angl. low ordering).
Pavyzdžiui dešimtainis skaičius 1316 turi tokią dvejetainę išraišką:![]() , kuri binariniame .roc
formato faile turėtų atrodyti taip: 00100100 00000101 00000000 00000000.
, kuri binariniame .roc
formato faile turėtų atrodyti taip: 00100100 00000101 00000000 00000000.
.roc formato faile pradžioje įrašomas bendras lyginamų porų skaičius, t.y. kaip taisyklė skaičius N * (N-1) / 2, kur N yra turimų duomenų bazėje skirtingų įrašų ( pvz. turimų veidų skaitmeninių nuotraukų ) skaičius. Toliau .roc formato faile įrašomi N * (N-1) / 2 sveikųjų skaičių ketvertukai: i, j, 0/1, s(x_i,x_j). Pirmasis ketvertuko skaičius i yra poros pirmojo elemento x_i indeksas. Antrasis skaičius j yra poros antrojo elemento x_j indeksas. Trečioje pozicijoje rašomas 1, jei pora (x_i,x_j) yra autentiška, t.y. id(x_i) = id(x_j), arba rašomas 0, jei pora (x_i,x_j) yra apsišaukėlių, t.y. id(x_i) nelygu id(x_j). Ketvirtoje pozicijoje rašomasis svarbiausias atpažinimo prasme skaičius, būtent apskaičiuoto panašumo įverčio reikšmė s(x_i,x_j). Kaip taisyklė, .roc formato failą sudaro tokie sveikųjų skaičių įrašai, kuriuos vaizdumo dėlei atskirsime kableliais ir sugrupuosime prasminėmis eilutėmis:
N(N-1)/2,
0, 1, id(x_0)==id(x_1), s(x_0,x_1),
0, 2, id(x_0)==id(x_2), s(x_0,x_2),
0, N-1, id(x_0)==id(x_(N-1)), s(x_0,x_(N-1)),
1, 2, id(x_1)==id(x_2), s(x_1,x_2),
1, 3, id(x_1)==id(x_3), s(x_1,x_3),
1, N-1, id(x_1)==id(x_(N-1)), s(x_1,x_(N-1)),
N-2, N-1, id(x_(N-2))==id(x_(N-1)), s(x_(N-2),x_(N-1)).
Čia id(x_i)==id(x_j) žymi 1, kai poros elementų identifikatoriai sutampa ir 0 priešingu atveju. Toks .roc formato failas užims 4 + 4 * N(N-1)/2 baitų.
Histograma. Tarkime turime apskaičiavę arba nuskaitę iš failo id(x_i)==id(x_j) ir s(x_i,x_j) reikšmes. Tuomet nesunku sudaryti autentiškų ir apsišaukėlių panašumo reikšmių histogramas. Histogramų sudarymo pseudokodas atrodys taip:
0. Masyvų inicijavimas:
genCount = new int[S+1], impCount = new int[S+1];
- Panašumo reikšmių pasikartojimo skaitliukų užpildymas:
for ( i = 0; i <N-1; i++)
for ( j = i+1; j <N; j++)
if ( id(x_i) == id(x_j)
genCount[s(x_i,x_j)]++
else impCount[s(x_i,x_j)]++.
- Skaitliukų procentinis normavimas, t.y. histogramų sudarymas:
totalGenCount = 0; totalImpCount = 0;
for ( s= 0; s <=S; s++)
{
totalGenCount += genCount[s];
totalImpCount += impCount[s];
}
genHist = new double[S+1], impHist = new double[S+1];
for ( s= 0; s <=S; s++)
{
genHist[s] = 100 * genCount[s] / totalGenCount;
impHist[s] = 100 * impCount[s] / totalImpCount;
}
Gauti genHist ir impHist histogramų masyvai yra pavaizduojami grafiškai abscisių ašyje atidedant panašumo reikšmes s, kurios gali kisti nuo 0 iki S, o ordinatė pavaizduojama stulpeliu, kurio aukštis proporcingas genHist[s] arba impHist[s] dydžiui. 4 pav. iliustruoja histogramų vizualizaciją. Šiuo atveju histogramos vaizduojamos ne stulpeliais, o grafikais gaunamais atidedant (s, genHist[s]) mėlynus (autentiški) ir (s, impHist[s]) raudonus ( apsišaukėliai ) taškus. Panašumo reikšmės apskaičiuotos taikant originalų rainelių atpažinimo algoritmą pritaikytą [ICE 2005] ICE 2005 left rainelių duomenų bazei. [Casia1] šaltinyje rasite nuorodą į kitą laisvai prieinamą rainelių duomenų bazę, kurią autoriai dažnai naudojama savo algoritmų testavimui. Vizualiai matyti, kad autentiškų porų panašumo įverčių histograma pasislinkusi dešiniau lyginant su apsišaukėlių porų histograma. To ir reikėtų tikėtis, nes kokybiškas atpažinimo algoritmas turėtų apskaičiuoti autentiškoms poroms kaip taisyklė didesnius panašumo reikšmes. Antra vertus abi histogramos dalinai kertasi, o tai reiškia, kad duotai ICE 2005 left duomenų bazei tiriamas rainelių atpažinimo algoritmas nėra idealus ir bus daroma FAR ar FRR tipo klaidų, tačiau sąlyginai šių klaidų procentas yra mažas, nes vizualiai histogramų persidengimo dalis užima nedidelį histogramomis ribojamų plotų dalį.
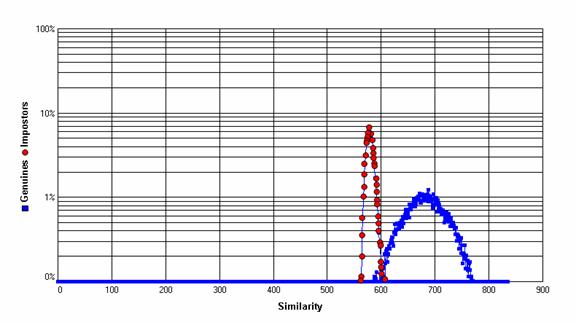
4 pav. Realaus atpažinimo algoritmo rainelių autentiškų (mėlyni taškai) ir apsišaukėlių ( raudoni taškai ) panašumo įverčių histogramos.
ROC kreivė. Beliko išsiaiškinti pagrindinį dalyką kaip praktiškai gauti ROC kreivę, kuri vizualizuoja atpažinimo algoritmo pritaikyto kokiai nors konkrečiai duomenų bazei kokybę. Aptariant autentiškų ir apsišaukėlių panašumo reikšmių histogramas mes išsiaiškinome, kad vizualiai galima įvertinti algoritmo kokybę. Tačiau toks kokybės įvertinimas yra gana abstraktus (histogramų grafikai persikloja mažai/stipriai), ROC kreivės pateikia visą spektrą konkrečių persiklojimų įverčių reikšmių. 5 pav. iliustruoja vieno ROC kreivės taško (FAR(s),FRR(s)) koordinačių FAR(s) ir FRR(s) sąsają su autentiškų ir apsišaukėlių porų panašumo reikšmių histogramomis.
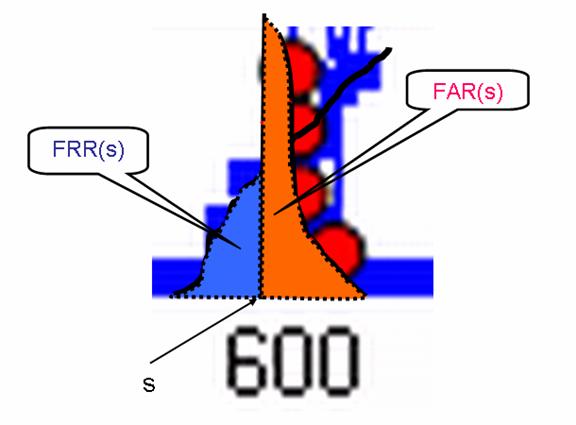
5 pav. Išdidinta persiklojančios 4 pav. histogramų dalis, lemianti FAR ir FRR klaidų kiekį. Fiksuotai panašumo įverčio reikšmei s, FAR(s) sutampa su rausvai nuspalvintos srities plotu išreikštu procentais atžvilgiu bendro apsišaukėlių histogramos ploto. Analogiškai FRR(s) sutampa su melsvai nuspalvintos srities plotu išreikštu procentais atžvilgiu viso autentiškų porų histogramos ploto.
Įvertinant praktiškai FRR(s) reikšmę patogu naudoti autentiškų porų panašumo reikšmių histogramą genHist, o FAR(s) apskaičiuojama panaudojant histogramos impHist reikšmes. Galima naudoti tokias apytiksliais plotų skaičiavimo išraiškas:
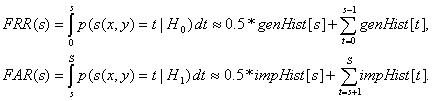
Šių formulių realizacijos pseudokodas atrodo taip.
0. FAR ir FRR masyvų inicijavimas ir kraštinių reikšmių priskyrimas:
far = new double[S+1], frr = new double[S+1];
far[S] = 0.5*impHist[S], frr[0] = 0.5*genHist[0].
- FAR ir FRR rekurentinis apskaičiavimas:
for ( s = S-1; s >=0; s--)
far[s] = far[s+1] + (impHist[s+1] + impHist[s]) / 2;
for ( s = 1; s <=S; s++)
frr[s] = frr[s-1] + (genHist[s-1] + genHist[s]) / 2;
- ROC kreivės pavaizdavimas, t.y. parametrinės kreivės {far(s), frr(s)} grafiko piešimas:
for ( s =0; s <= S; s++)
plot( far[s], frr[s])
Atkreipkite dėmesį, kad skaičiuojant far(s) ir frr(s) reikšmes mums neprireikė plotų normalizacijos, kadangi histograma jau yra normalizuota taip, kad visų jos elementų suma lygi 100 (%).
6 pav. iliustruoja tokiu būdu gaunamos ROC kreivės grafiką. Atkreipkite dėmesį į pateikiamą papildomą informaciją. Tekstine forma yra užrašyta kiek viso buvo lyginama porų (šiuo atveju 1166628 ), kiek tarp jų buvo apsišaukėlių ( 1151975 ), kiek autentiškų ( 14653 ), lygios klaidos ( Equal Error ) reikšmė ( 2.14 % ), Zero FAR = 8.93 % (t.y. nedarant nei vieno klaidingo pripažinimo apsišaukėlių autentiška pora verifikuojant autentiškas poras yra daroma 8.93 % klaidų, pateikiamos FRR reikšmės fiksuotoms standartinėms FAR reikšmėms: 0.001 %, 0.01 %, 0.1%, 1 % ir t.t. Atkreipkite dėmesį, kad FAR ir FRR grafiko ašys naudoja logaritminę skalę. ROC kreivės vaizdavimas loglog skalėje yra gana įprastas, nes dažnai šiuolaikinių verifikacijos algoritmų kokybė būna gana aukšta ir logaritminės ašys tokiu atveju patogios vaizduojant mažus FAR ir FRR klaidų dažnius.
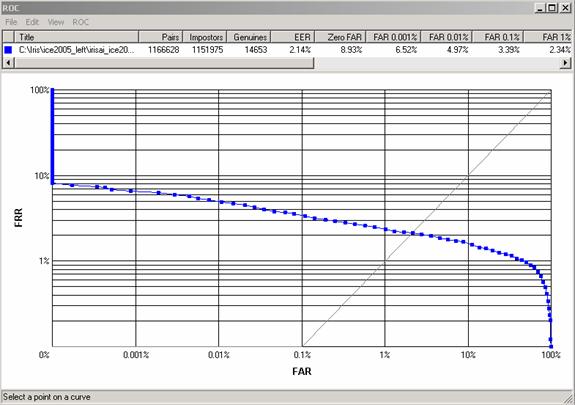
6 pav. ICE 2005 left rainelių duomenų bazės atpažinimo ( verifikacijos ) ROC kreivė. ROC kreivės programos autorius Justas Kranauskas, MIF doktorantas.
Atliekant praktinę atpažinimo kokybės vizualizavimo užduotį jums bus pateikti .roc formato realiu atpažinimo algoritmo duomenų pagrindu suformuoti duomenų failai. Reikalavimai jūsų programai
1. Programavimo kalbą ir grafines vaizdavimo priemones renkatės laisvai.
2. Nuskaitote pateikto neurotechnologija .roc formato failo duomenis.
3. Sudarote apsišaukėlių ir autentiškų porų panašumo įverčių histogramas ir pavaizduojate jas grafiškai.
4. Apskaičiuojate FAR(s) ir FRR(s) klaidų reikšmes ir pavaizduojate jas ROC kreive.
5. Sudarote galimybę vartotojui pasirinkti logaritmines arba įprastas ROC kreivės ašis. (neprivalomas)
6. Pavaizduojate duotų duomenų ROC kreives ir vizualiai įvertinate Zero FAR, EER (Equal Error Rate), Zero FRR, FRR reikšmes, kai FAR = 0.001%, 0.01%, 0.1% arba 1% ir FAR, kai FRR = 0.001%, 0.01%, 0.1% arba 1%.
7. Žodžiu palyginate dviejų atpažinimo algoritmų kokybę remiantis jų ROC kreivėmis.
Projektas atliekamas ne pratybų metu suderinus iš anksto su dėstytoju jo pasirinkimą, detales ir vertinimo skalę. ROC projekto tikslas padaryti .roc failų peržiūros instrumentą. Reikalavimai instrumentui.
1. Programavimo kalbą ir grafines vaizdavimo priemones renkatės laisvai. Projekto rezultatas turi būti vykdomasis failas.
2. Instrumentas turi nuskaityti pateikto neurotechnologija .roc formato failo duomenis ir atlikti RocViewer.exe programos funkcijas.
3. Papildomai jūsų programa turi sugebėti nuskaityti pateikiamus *.list formato failus. Šio formato failų pavyzdžiai: galery.list, probe.list.
4. Panaudojant *.roc ir *.list failuose esančią informaciją turi būti suteikiama galimybė vartotojui patogiai išsirinkti norimus failus ir atliekama išsirinktų failų vizualizacija.
Past. Tekstas paruoštas naujai, todėl atsiprašau už gramatines ir stiliaus klaidas ir prašyčiau informuoti mane ( algirdas_bastys eta yahoo taskas com ) apie pastebėtus netikslumus.
[Wikipedia ROC] Receiver operating characteristic, http://en.wikipedia.org/wiki/Receiver_operating_characteristic
[Magnificent ROC] The magnificent ROC,
http://www.anaesthetist.com/mnm/stats/roc/Findex.htm
[ICE 2005] "Face and Iris Evaluations at NIST," presentation by P. J. Phillips atCardTech/SecurTech 2006, 3 May 2006, San Francisco, http://iris.nist.gov/ice/presentations.htm
[Casia1]. Chinese Academy of Sciences Institute of Automation Iris Database 1.0, available online at: http://www.sinobiometrics.com, 2003.
