Tiesinė prognozė (angl. LPC - LinearPredictionCoefficients arba LinearPredictionCoding) yra vienas galingiausių signalų analizės metodų. Ypač jis gerai užsirekomendavo kalbos analizėje, tiesine prognoze paremtas kalbos kodavimas duoda geriausius kalbos ir kompresijos kokybės parametrus. Šiuo metodu gaunami kalbą aprašantys parametrai, jų skaičius yra nedidelis ir jie apskaičiuojami greitai. Čia aprašysime pagrindines tiesinės prognozės metodo idėjas ir aptarsime kai kurias metodo realizacijos ypatybes.
LPC metode daroma prielaida, kad kalbos signalas yra sužadinamas garso šaltiniu patalpintu kintamo skerspjūvio vamzdelio gale. Sužadintos garso bangos plinta vamzdeliu ir išsiveržia į aplinką priešingame gale. Pas žmogų garso šaltinis yra plaučiuose sudarytas atmosferinis viršslėgis ir virpančios balso stygos. Šis šaltinis charakterizuojamas intensyvumu (garsumu) ir dažniu (pagrindiniu tonu). Gerklės ir burnos kalbos traktas formuoja kintamo skersmens vamzdelį. Kalbos traktas charakterizuojamas rezonansiniais dažniais, vadinamais formantėmis.
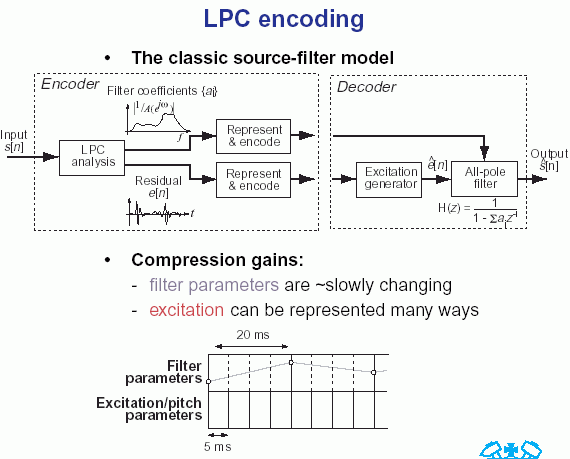
Tiesinė prognozės metodu yra įvertinamos formantės, atskiriant jas nuo kalbą generuojančio šaltinio, lemiančio kalbos garsumą ir toną. Formančių eliminavimas iš kalbos signalo kartais vadinamas atvirkštiniu filtravimu, ir likęs signalas vadinamas liekamuoju.
Skaičiai aprašantys formantes ir liekamasis signalas gali būti saugojami ir siunčiami atskirai. Kalbos sintezavimas tiesinės prognozės metodu gaunamas apgręžiant metodą: liekamasis signalas tampa kalbos signalą generuojančiu šaltiniu, o iš formančių gaunamas filtras, atspindintis kalbos trakto geometriją. Filtruojant liekamąjį signalą ir gaunamas sintezuotas garsas.
Kadangi kalbą generuojantis traktas kinta laike, tiesinė prognozė atliekama trumpais laiko tarpais, vadinamais fragmentais, langais (frames). Kaip taisyklė, vienos sekundės trukmės kalbos signalas skaidomas į 30-50 langų.
Pagrindinė LPC metodo problema yra įvertinti formantes remiantis
įrašytu kalbos signalu. Metodu tikslas yra gauti tam tikrą diferencialinę lygtį, kurios esmė yra išreikšti kuo tiksliau eilinę
garso slėgio imtį remiantis keliom prieš tai žinomom kalbos
signalo reikšmėm. Kadangi naudojama tiesinė aproksimacija, tai gaunama
skirtuminė diferencialinė lygtis yra vadinama
Diferencialinės išraiškos koeficientai vadinami prognozės (tiesinės) koeficientais. Šie koeficientai aprašo formantes,
taigi metodo esmė yra apskaičiuoti tiesinės prognozės koeficientus.
Formulės apskaičiuoti LPC koeficientus yra gaunamos minimizuojant
liekamojo signalo vidutinę kvadratinę paklaidą.
Rezultate yra gaunama atžvilgiu prognozės koeficientų
tiesinė algebrinių lygčių sistema. Praktiškai tenka spręsti tokias problemas:
Gali atrodyti keista, kad kalbos signalas gali būti aprašytas
tokiu paprastu vamzdelio modeliu. Kad toks paprastas modelis galiotų,
vamzdelis turi neturėti nei vieno išsišakojimo.
Kiekviena šaka aprašoma antirezonansiniais dažniais, kurie pasižymi tam tikro ilgio bangų slopinimu. Matematine prasme vamzdelį su išsišakojimais geriau aprašinėti tokiu modeliu, kuris leistų reguliuoti
signalo nulius spektro srityje.
Įprasti balsiai gerai aprašomi paprastu kintamo skerspjūvio vamzdeliu.
Tačiau nosiniai garsai, kurių suformavime aktyviai dalyvauja
šoninis nosies ertmės kanalas, reikalauja kiek sudėtingesnio
modelio. Tačiau praktiškai į tai dažnai neatsižvelgiama ir problemos
sprendimas nukeliamas į liekamojo signalo valdymą.
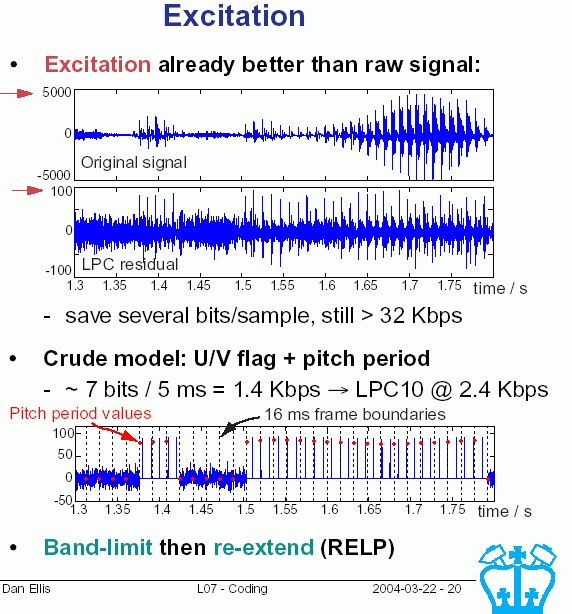
Jei prognozės koeficientai gerai apskaičiuoti, kita yra paprasta:
atlikti atvirkštinį filtravimą ir gauti gryną liekamąjį narį.
Remiantis gautu liekamuoju nariu įvertinamas pagrindinis tonas
ir jo galia, bei jie užkoduojami (įsimenami).
Tačiau kai kurie priebalsiai yra suformuojami turbulentinėmis
oro srovėmis, dėl ko gaunasi frikatyviniai (šnypščiamieji) ir
sprogstamieji garsai.
Kiekvienam fragmentui reikia nuspręsti su kokiu garsu dirbama.
Jei tai kvaziperiodinis - įvertinti pagrindinį toną; bet kuriuo
atveju įvertinti liekamojo nario galią. Ši kokybinė informacija apie
garsą taip pat yra užkoduojama (glaustai užrašoma). Sintezės metu
ši informacija naudojama imituojant garso šaltinio modelį.
LPC-10e standarte 1 žymimi vokaliniai fragmentai,
LPC-10e sugeba perteikta geros kokybės kalbą 2400 bitų per sekundę greičiu.
Deja, ne viskas taip paprasta. Daugelis garsų nėra grynai vokaliniai arba nevokaliniai.
Pavyzdžiui, r, z, v turi ir balsio ir priebalsio bruožų.
Tokius garsus generuodami dviejų būsenų tiesinės prognozės metodu
paremtu sintezatoriumi negausime geros garso kokybės.
Kita problema yra mažas formančių kiekis, aprašomas tiesinės
prognozės koeficientais. Tai pasireiškia tuo, kad dalis garso informacijos pereina į liekamąjį narį. Pavyzdžiui, nosiniai garsai
pasižymi antirezonansiniais dažniais ir ši informacija persikelia
į liekamąjį narį. Liežuvio sudaromi tarpai veikia panašiai
kaip ir nosies ertmės. Dėl to praktiškai visi garsai
vien tik rezonansiniais dažniais (formantėmis) aprašomi netiksliai.
Todėl liekamasis narys yra svarbus ir menkas jo aprašymas negali garantuoti
geros sintezuojamo garso kokybės.
Geriausia kokybė pasiekiama, jei, kartu su tiesinės prognozės koeficientais, pilnai perduotume ir liekamąjį narį.
Deja visa esmė yra suspausti kalbos signalą; jei perduotumėme pilnai
ir liekamąjį narį, tai iš esmės perduodamas signalas užimamų bitų
skaičiumi mažai skirtųsi nuo pradinio kalbos signalo.
Taigi reikia ieškoti būdų kaip glaustai perduoti esminę informaciją
apie liekamąjį narį.
Yra aibė pasiūlymų kaip koduoti liekamąjį narį.
Tai labai svarbi vieta lemianti kompresijos ir sintezuojamo signalo
kokybės santykį.
Dabar labai populiarios yra kodų lentelės, tai yra tam tikri
dažnai pasitaikantys liekamųjų signalų pavyzdžiai, kurių sudarymo principai ir lemia konkretaus LPC sintezatoriaus ypatybes.
Dirbant su kodų lentelės, kodavimo metu yra parenkamas
iš lentelės pavyzdys, kuris mažiausiai skiriasi nuo
gautos tuo momentu konkrečios paklaidos ir įsimenamas tik
išrinkto lentelės kodo numeris. Sintezavimo metu pagal numerį iš
kodų lentelės pasiimamas kodas su atitinkamu numeriu ir vėliau jis
naudojamas sužadinti tiesinės prognozės koeficientais aprašomam
filtrui. Tokios schemos vadinamos CELP -
CodeExcitedLinearPrediction.
Kad CELP dirbtų gerai, kodų lentelė turi būti pakankamai turtinga, kad iš jos būtų galima parinkti artimą
įvairiems liekamiesiems signalams. Bet jei lentelė yra didelė,
tampa sunku parinkti artimą ir vėl mažėja kompresijos laipsnis.
Didžiausia problema yra, kad skirtingų kalbos fragmentų pagrindiniams
tonams reikės skirtingų kodų lentelių.
Šią problemą galima spręsti sudarant dvi mažas kodų lenteles vietoje vienos didelės. Viena lentelė yra sudaroma iš anksto LPC sistemos kūrėjo ir joje saugomos vieno periodo
(laiko tarpo tarp balso stygų susitraukimo) trukmės liekamieji nariai.
Kitas lentelė yra adaptyvi. Ji inicializuojama tuščia aibe ir yra
užpildoma palaipsniui, saugant paskutinių įvairios trukmės liekamųjų narių pavyzdžius.
Naudojant tokį CELP metodą
gaunama gera natūraliai skambanti kalba su sąnaudom
4800 bitai per sekundę.
Tarkime {xn}n=0,...,N-1
yra signalo fragmento duomenys.
Pažymėkime {am}1<m<M tiesinės
prognozės koeficientus. Čia M žymi ieškomų
prognozės koeficientų skaičių. Patogumo dėlei pažymėsime
a0=1. Pagal tiesinės prognozės metodą eilinė duomenų
reikšmė xn yra aproksimuojama keletu prieš tai žinomų
duomenų reikšmių tiesine išraiška.
Tiesinės išraiškos koeficientai pasirinktam duomenų fragmentui
nekeičiami (jie nepriklauso nuo indekso n).
Taigi, pažymėję tiesinės prognozės paklaidą
en,
gausime tokią išraišką:
xn = S
1<m<M amxn-m+
en.
Šioje išraiškoje nenurodėme indekso n kitimo sritį. Užrašyti
n=0,...,N-1 būtų ne visai tikslu, nes pradiniams n<M,
duomenys xn-m, kai m>M, būtų neapibrėžti.
Populiariausi yra tokie šios problemos sprendimai būdai:
Dirbant su kalbos signalu, pirmojo fragmento atveju galima
naudoti 1-ąjį variantą, o vėliau, kai jau žinomi prieš fragmentą
einantys duomenys, galima pereiti prie 3-iojo varianto.
Err = Sn
(xn-
S1<m<M amxn-m)2
(=Sn
(en)2).
Čia n kitimo srities vėl nenurodėme
dėl anksčiau minėtų priežasčių. Minimizuojant funkciją Err
reikia apskaičiuoti jos išvestines
kintamųjų amatžvilgiu ir prilyginti jas 0.
Taip gaunama tokia tiesinių lygčių sistema:
Sn
xn-k(xn-
S1<m<M
amxn-m) = 0, k=1,2,...,M.
S1<m<M
amRk-m = Rk, k=1,2,...,M.
Rn = Sk
xn+kxk.
Tiesinės prognozės koeficientų metodą nesunku apibendrinti
plokštumos taškams aproksimuoti. Prognozės metodo tikslas rasti tokius kompleksinius
skaičius am, kad įstačius juos į prognozės paklaidos
išraiškas
zn - S
1<m<M amzn-m =
en
gautume minimalią bendrą paklaidą, t.y. reikia minimizuoti
Err = Sn
|zn-
S1<m<M amzn-m|2
(=Sn
|en|2).
Sn
[ (xn-k+Iyn-k)((xn-Iyn) -
S1<m<M
(am-I
bm)(xn-m-Iyn-m)) +
Sn
[ (xn-k+Iyn-k)((xn-Iyn)-
S1<m<M
(am-I
bm)(xn-m-Iyn-m)) -
k=1,2,...,M.
Jei zn=0, kai n<0, tai
pastarąją lygčių sistemą galima perrašyti taip:
S1<m<M [
amRe(Rm-k) +
bmIm(Rm-k) ]
= Re(R-k),
S1<m<M [
amIm(Rm-k) -
bmRe(Rm-k) ]
= Im(R-k),
k=1,2,...,M.
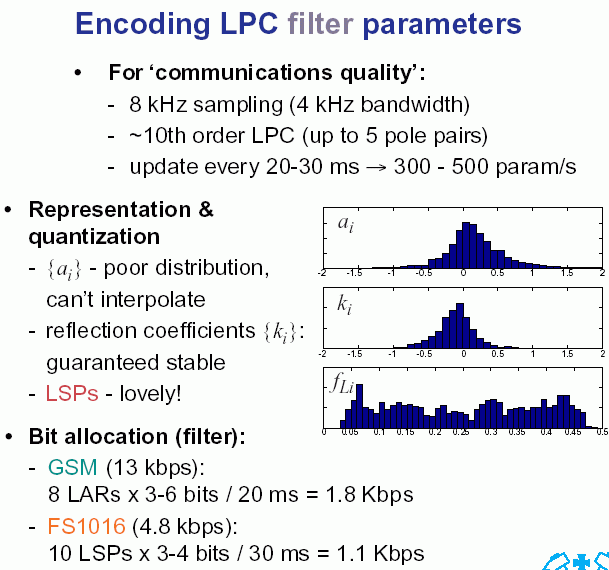
Naudojami keli matricos koeficientų gavimo metodai
(autokoreliacijos, kovariacijos, rekursyvinės gardelės), kurie
garantuoja sprendinio vienatį ir skaičiavimų efektyvumą.
Niuansai: vamzdelis nelygus vamzdeliui
Šaltinio kodavimas
Laimei, tiesinės prognozės lygčiai yra nesvarbu kokios rūšies
garsas yra aproksimuojamas (kvazi-periodinis ar chaotinis).
Niuansai: balsiai - ne balsiai, priebalsiai - nepriebalsiai
Liekamojo signalo (prognozės paklaidos) kodavimas
Matematinė dalis
Lygtis tiesinės prognozės koeficientams
{am}1<m<M
gaunamos minimizuojant atžvilgiu prognozės koeficientų
(vidutinę) kvadratinę paklaidą, t.y.
Plokštumos taškų tiesinė prognozė
Tarkime plokštumos taškai žymi spausdintinio
simbolio kontūro taškus ir sunumeruoti kontūro apėjimo prieš arba pagal
laikrodžio rodyklę tvarka. Tikėtina, kad eilinį kontūro tašką galima
neblogai aproksimuoti tiesiniu dariniu sudarytu iš prieš tai jau žinomų
kontūro taškų. Eilės tvarka pažymėtus kontūro taškus patogu laikyti
kompleksiniais skaičiais
zn = xn+Iyn,
n=0,1,...,N-1, (I menamasis vienetas, t.y. šaknis iš -1).
Prognozės koeficientus am, m=1,2,...,M taip pat
laikysime kompleksiniais skaičiais:
am = am+
Ibm.
(xn-k-Iyn-k)((xn+Iyn)-
S1<m<M
(am+I
bm)(xn-m+Iyn-m)) ] = 0,
(xn-k-Iyn-k)((xn+Iyn)-
S1<m<M
(am+I
bm)(xn-m+Iyn-m)) ] = 0,
Čia Rn = Sk zk+nConj(zk) ( = Sk (xk+n + Iyk+n)(xk - Iyk) ).
Išsprendę gautą tiesinę lygčių sistemą rasime nežinomuosius am ir bm, m=1,2,...,M, ir kompleksinius tiesinės prognozės koeficientus
am = am + Ibm.
Analizuojant gautą lygčių sistemą atžvilgiu nežinomųjų, kurie ir yra tiesinės prognozės koeficientai, matyti kad:
Lygčių sistemom su tokia specifika spręsti egzistuoja efektyvus metodas, vadinamas autorių vardu Levinson-Durbin algoritmu. Metodas rekursyviai ieško tiesinės prognozės koeficientus.
ami = ami-1 - kiai-mi-1 ;
Ei = (1-(ki)2) Ei-1;
Atlikus paskutinę iteraciją gaunamas galutinis sprendinys:
am = (aM)m, 1<m<M .
Levisono-Durbin algoritmo sudėtingumas yra O(M2) eilės. Tai eile mažiau, nei tiesioginio lygčių sistemos sprendimo metodo sudėtingumo, kuris gaunasi lygčių sistemą sprendžiant kintamųjų eliminavimo metodu. Grubiai kalbant, kadangi Tioplico matricai aprašyti pakanka tik jos pirmosios eilutės elementų, tai galima tikėtis, kad specifinei lygčių sistemai spręsti kurios koeficientai prie nežinomųjų sudaro Tioplico matricą, galima surasti efektyvų sprendimo metodo. Levisono-Durbin algoritmas šį teiginį patvirtina.
Kitas Levisono-Durbin algoritmo privalumas yra tai, kad rekurentinių skaičiavimų eigoje mes paeiliui surandame tiesinės prognozės koeficientus eilės M=1, M=2 ir t.t. Koeficientai ki turi fizikinę interpretaciją ir yra vadinami atspindžio koeficientais. Atspindžio koeficientų modulis turi neviršyti 1; jei skaičiavimų eigoje gavote ki reikšmes nepatenkančias į intervalą [-1;1], tai arba tai atsitiko dėl skaičiavimo paklaidų arba formulės pagal kurias skaičiavote autokoreliacijos koeficientus Rm davė fizikine prasme blogą rezultatą.
Kokias N ir M reikšmes pasirinkti?
Laikantis taisyklės, kad vienos sekundės trukmės kalbos signalas
būtų skaidomas į 30-50 langų, gauname, jog N reikšmė priklauso
nuo signalo imčių dažnio FS (FrequencySampling - kiek kartų
per sekundę įrašoma garso slėgio reikšmių).
Tipinės FS reikšmės yra
Tarkime FS=22050. Tuomet galima pasirinkti N=FS/30=735 ar N=FS/50=441. Tačiau praktiškai geriau imti N sveikąjį dvejeto laipsnį, kad būtų naudotis greitais koreliacijos apskaičiavimo algoritmais. Šiuo atveju būtų tikslinga imti N=512.
Plokštumos taškų atveju reikėtų kontūrą suskaidyti į atskiras dalis, pvz. grupes atskirti kampiniais ar kitais ypatingais kontūro taškais, ir aproksimuojant kiekvienos grupės taškus naudoti neaukštos eilės (M=2-4) tiesinės prognozės modelį. LPC metodas yra pagrindinė efektyvi kalbos signalų kompresijos priemonė. Plačiau apie šį metodą galima paskaityti nurodytoje literatūroje.

LPC10e ir CELP programų kodai prieinami ftp://ftp.super.org/pub/speech/.
2004 m. kovo 22 d.