Dauguma jūsų jau mokykloje žinojote kaip konstruoti
elektrines grandines. Bet kokios paprastos elektrinės
schemos pagrindas yra trys baziniai elementai: varža, kondensatorius
ir ritė. Šie trys elementai skirtingai keičia grandine tekančią
srovę ir įtampą, todėl jie yra elektrinių schemų konstrukcijų baziniai elementai.
Signalų analizėje yra analogijų su elektrinėmis schemomis.
Tai ypač taikytina filtravimo operacijai. Atskirus
filtrus galima jungti ir nuosekliai ir lygiagrečiai; žemųjų,
vidurinių ir aukštųjų dažnių filtrai specifiškai keičia signalus.
Čia pakalbėsime apie konvejerinę signalo apdorojimo schemą
(angl. pipeline - "pypkės rūkymas perduodant ją grandine")
skirtą kepstro koeficientams skaičiuoti.
Kalbos signalo kepstro koeficientai teikia vertingą informaciją
apie pagrindinio tono arba balso stygų svyravimų dažnį.
Periodiškai virpant balso stygom garso slėgis tai sustiprėja,
tai susilpnėja. Tik atsivėrus balso stygom garso slėgis pradeda stiprėti,
ir atvirkščiai - kai balso stygos susispaudžia - garso slėgis
sumažėja. Tai iliustruoja "a" balsio garso slėgio grafikas:
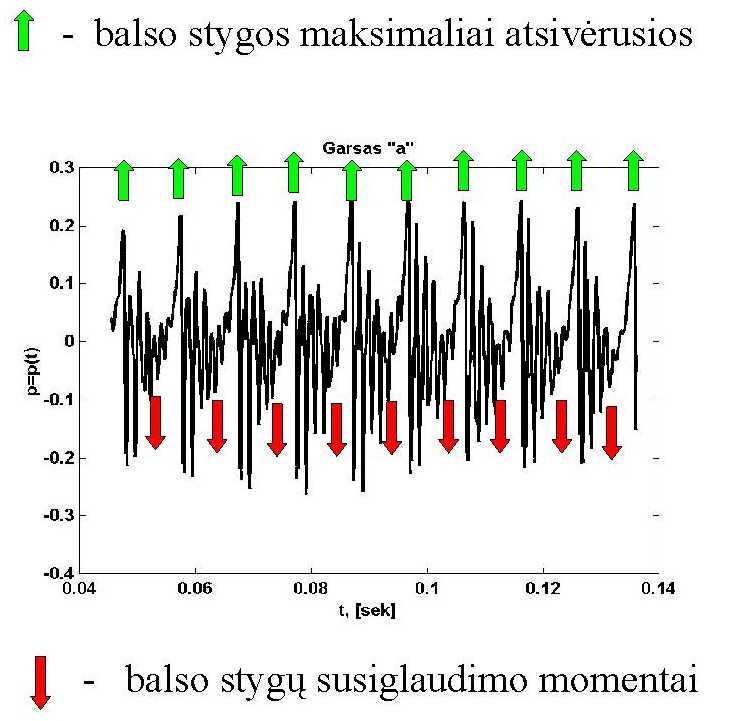
Kyla klausimas - kaip įvertinti balso stygų susitraukimo dažnį kompiuteriu.
Aišku, galima mėginti tiesiogiai vertinti garso slėgio lokalius maksimumo ar
minimumo taškus ir kurti kokį nors algoritmą, kuris įvertintų
ar eilinis lokalus ekstremumas žymi balso stygų maksimalaus atsivėrimo
momentą. Tačiau tokį metodą sunku realizuoti, jis duosi nelabai tikslų
ir patikimą rezultatą.
Apskaičiuokime to paties signalo diskrečiąją Furjė transformaciją
ir pavaizduokime jos modulio kvadratą (energijos tankis dažnio srity):
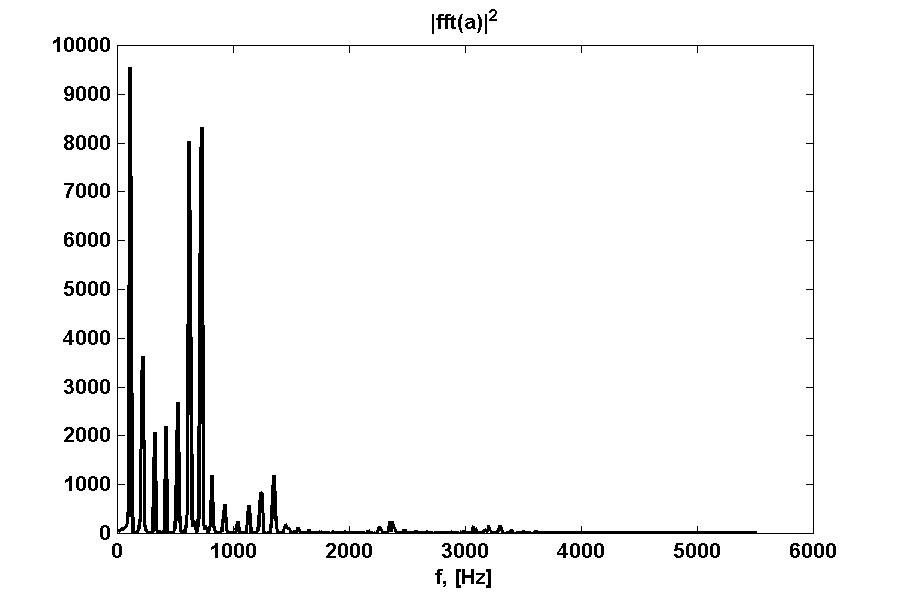
Piešinyje aiškiai matyti periodiškai pasikartojanti spektre teigiamų
pusbangių seka. Šis periodiškumas spektre atsiranda dėl periodinio
balso stygų virpesio. Jei vidutinį laiko tarpą tarp gretimų stygų susitraukimo
momentų pažymėti T [sek] ir analogišką periodą to paties balsio spektro
F [1/sek], tai tarp jų bus paprastas ryšys:
T*F = 1.
Balsio periodiškumas dažnio srityje dar geriau matysis, jai apskaičiuosime
jo spektro modulio kvadrato logaritmą:
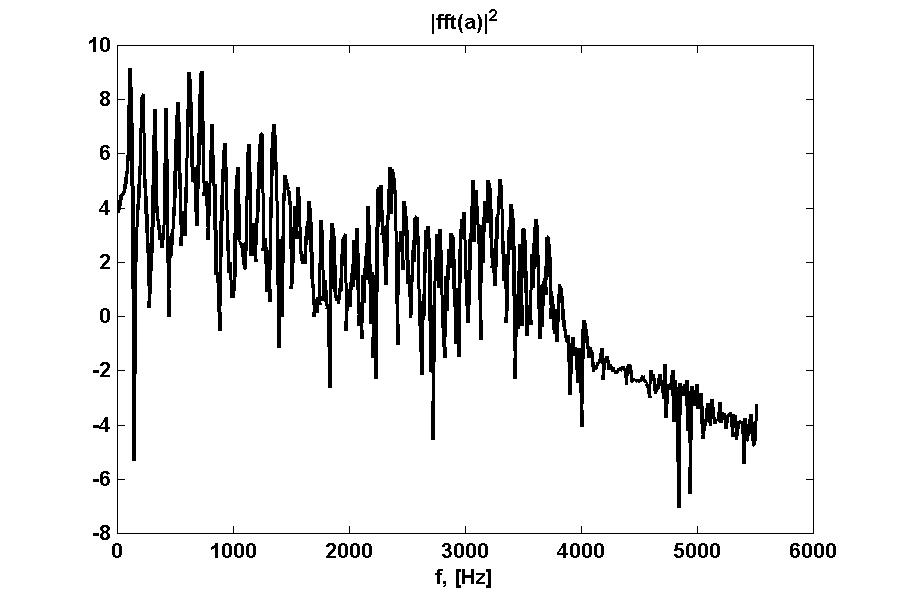
Taip atsitinka dėl to, kad realiai matuojami signalai yra glodūs,
o glodžių signalų Furjė transformacija greitai artėja į nulį.
Logaritmo funkcija šį artėjimą niveliuoja. Yra ir subtilesnių priežasčių,
dėl ko yra naudinga apskaičiuoti spektro galingumo logaritmą, bet
apie tai kiek vėliau.
Iki kepstro koeficientų liko tik vienas žingsnis.
Ap. Diskrečiojo signalo x kepstro koeficientais
c vadinama jo diskrečiosios Furjė transformacijos logaritmo atvirkštinė
Furjė transformacija, t.y.
c = ifft(log(|fft(x)|^2))
fft - žymi "Fast Fourier Transform" procedūrą. Jos ir kitų giminingų
jai metodų java klasę galite pasiimti čia:
fft.java; pagalbinė - my.java.
Angliškas cepster ir lietuviškas pavadinimas atspindi
naudojamos procedūros eigą: Furjė tr. - atvirkštinė Furjė tr. ir
spect-r - atvirkščiai cepst-er
(spek-tras - atvirkščiai keps-tras).
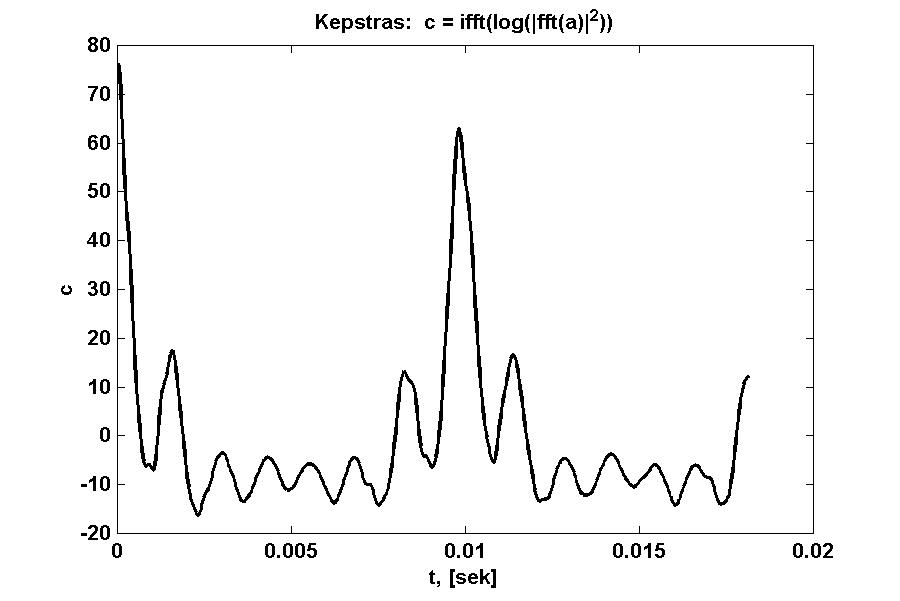
Pateiktame kepstro koeficientų grafike matyti ryškus maksimumas apie 0.01 sek.
Kodėl kepstro koeficientų abscisių ašį žymime "t, [sek]"? Taip yra dėl to,
kad pradinio signalo abscisių ašis yra laikas, Furjė transformacijos
modulio kvadrato logaritmo - dažnis f, o apskaičiavę
atvirkštinę - vėl grįžtame prie laiko skalės.
Natūraliai kyla klausimas kodėl kepstro koeficientai išryškina periodo reikšmę.
Jei signalas x=x(t) yra beveik periodinis
(pvz. garso slėgis atitinkantis balsės laikotarpį), tai jį galima išskaidyti
į sąsūkos T periodo žadinimo signalo
p(t) = Sn d(t-nT)
su vieno periodo impulso forma a(t) sumą su
paklaidos ("triukšmo") e(t) signalu.
Todėl
x(t) = (p*a)(t) + e(t).
Kuo periodiškumas reguliaresnis tuo e(t) paklaida
ir jos Furjė transformacija bus mažesni. Kadangi sąsūkos Furjė transformacija
yra lygi sąsūkos dėmenų Furjė transformacijų sandaugai, tai galios apytikslė
lygybė
|X(f)| @ |P(f)A(f)|.
Sandaugos |P(f)A(f)| logaritmas išsiskaido į logaritmų sumą ir tokiu būdu gausime
log |X(f)| @ log |P(f)| + log|A(f)|.
T-periodinės funkcijos p Furjė transformacija yra 1/T periodinė, tiksliau
P(f) = Sn d(f-n/T),
todėl Furjė transformacijos modulio logaritmo grafike matyti periodiškai
pasikartojantys maksimumai.
Reguliaraus periodo impulso spektro energija sukoncentruota arti nulinio dažnio
f=0 ir neturi išreikštos periodinės struktūros.
Todėl atvirkštinėje Furjė transformacijoje su t artimiems periodui T
dominuoja periodinės dalies log(|P(f)|) komponentė.
Taigi kepstro koeficientų pirmojo arti 0 ryškaus lokalaus maksimumo abscisė
gerai aproksimuoja beveik periodinio signalo periodo vidutinę reikšmę T.
Tarkime signalo imčių dažnis F=44100 [tšk/sek], o vidutinė periodo reikšmė
T=0.01 sek. Tuomet diskrečiojo kepstro, kuris gaunamas
vietoje tolydžiųjų Furjė transformacijų naudojant diskrečiąsias,
koeficientas cn su indeksu n=44100*0.01=441 turėtų būti
arti lokalaus maksimumo.
Pirmųjų kepstro koeficientų (20-30) Furjė transformacija
neblogai aproksimuoja suglodintą spektro logaritmą.
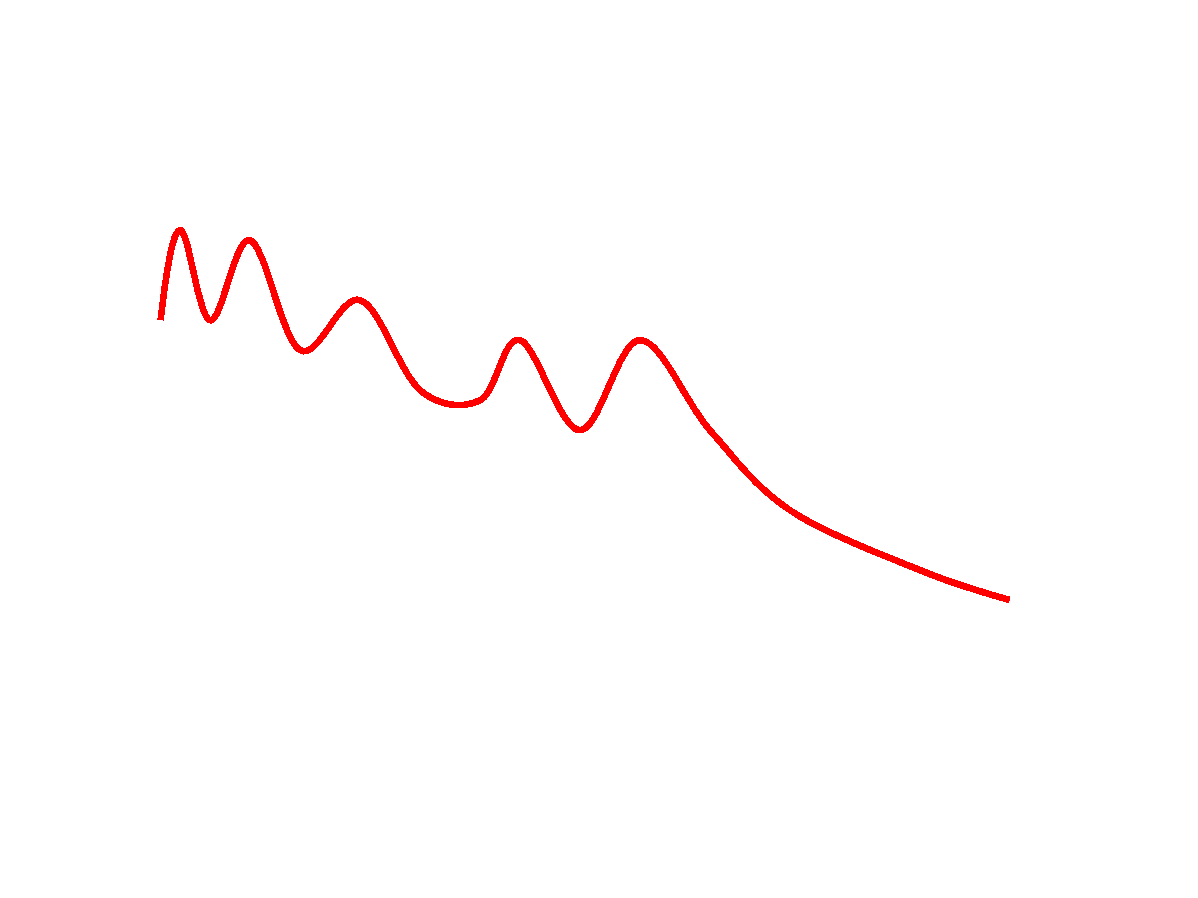
Todėl pirmieji kepstro koeficientai gana dažnai laikomi kalbos signalo
požymiais.
Logika tokia: kadangi žmogus garsą atpažįsta pagal jo spektrą,
o pirmieji 20-30 koeficientų netiesiogiai atspindi signalo spektro formą,
tai šiuose kepstro koeficientuose glūdi pakankamai informacijos, kad iš
jų būtų galima atpažinti garsą.




